Oto jak te dwa podejścia będą fizycznie reprezentowane w bazie danych:
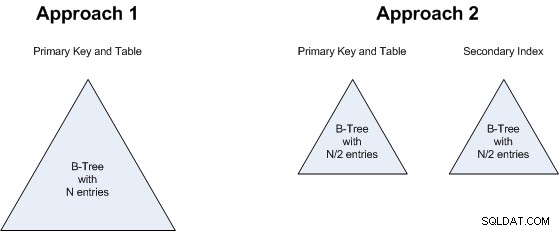
Przeanalizujmy oba podejścia...
Podejście 1 (oba kierunki zapisane w tabeli):
- PRO:Prostsze zapytania.
- CON:Dane mogą zostać uszkodzone przez wstawienie/aktualizację/usunięcie tylko w jednym kierunku.
- MINOR PRO:Nie wymaga dodatkowych ograniczeń, aby zapewnić, że przyjaźń nie może zostać zduplikowana.
- Potrzebna dalsza analiza:
- TIE:Jeden indeks okładki w obu kierunkach, więc nie potrzebujesz dodatkowego indeksu.
- TIE:Wymagania dotyczące pamięci.
- TIE:Wydajność.
Podejście 2 (tylko jeden kierunek zapisany w tabeli):
- CON:Bardziej skomplikowane zapytania.
- PRO:Nie można uszkodzić danych, zapominając o obsłudze przeciwnego kierunku, ponieważ nie ma przeciwnego kierunku .
- POMNIEJSZA WALKA:Wymaga
CHECK(UID < FriendID), więc ta sama przyjaźń nigdy nie może być reprezentowana na dwa różne sposoby, a klawisz(UID, FriendID)może wykonać swoją pracę. - Potrzebna dalsza analiza:
- TIE:Do pokrycia
potrzebne są dwa indeksy oba kierunki zapytań (indeks złożony na
{UID, FriendID}i złożony indeks na{FriendID, UID}). - TIE:Wymagania dotyczące pamięci.
- TIE:Wydajność.
- TIE:Do pokrycia
potrzebne są dwa indeksy oba kierunki zapytań (indeks złożony na
Punkt 1 ma szczególne znaczenie. MySQL/InnoDB zawsze klastry dane, a indeksy pomocnicze mogą być kosztowne w tabelach klastrowych (patrz „Wady klastrowania” w ten artykuł ), więc mogłoby się wydawać, że indeks wtórny w podejściu 2 zjadałby wszystkie zalety mniejszej liczby wierszy. Jednak , indeks pomocniczy zawiera dokładnie te same pola co podstawowy (tylko w odwrotnej kolejności), więc w tym konkretnym przypadku nie ma narzutu na przechowywanie. Nie ma też wskaźnika do sterty tabeli (ponieważ nie ma sterty tabeli), więc prawdopodobnie jest to nawet tańsze pod względem przechowywania niż normalny indeks oparty na stercie. I zakładając, że zapytanie jest objęte indeksem, nie będzie też podwójnego wyszukiwania, które normalnie jest skojarzone z indeksem pomocniczym w tabeli klastrowej. Tak więc jest to w zasadzie remis (ani podejście 1, ani podejście 2 nie ma znaczącej przewagi).
Punkt 2 wiąże się z punktem 1:nie ma znaczenia, czy będziemy mieli B-drzewo o N wartościach, czy dwa B-drzewa, każde z N/2 wartościami. To też jest remis:oba podejścia zużyją mniej więcej taką samą ilość pamięci.
To samo rozumowanie dotyczy punktu 3 :czy przeszukujemy jedno większe B-Tree, czy 2 mniejsze, nie ma większego znaczenia, więc jest to również remis.
Tak więc, ze względu na niezawodność i pomimo nieco brzydszych zapytań i potrzeby dodatkowego CHECK , wybrałbym podejście 2.