Geolokalizacja dużej liczby postów na podstawie adresów IP. (880 000 wierszy)

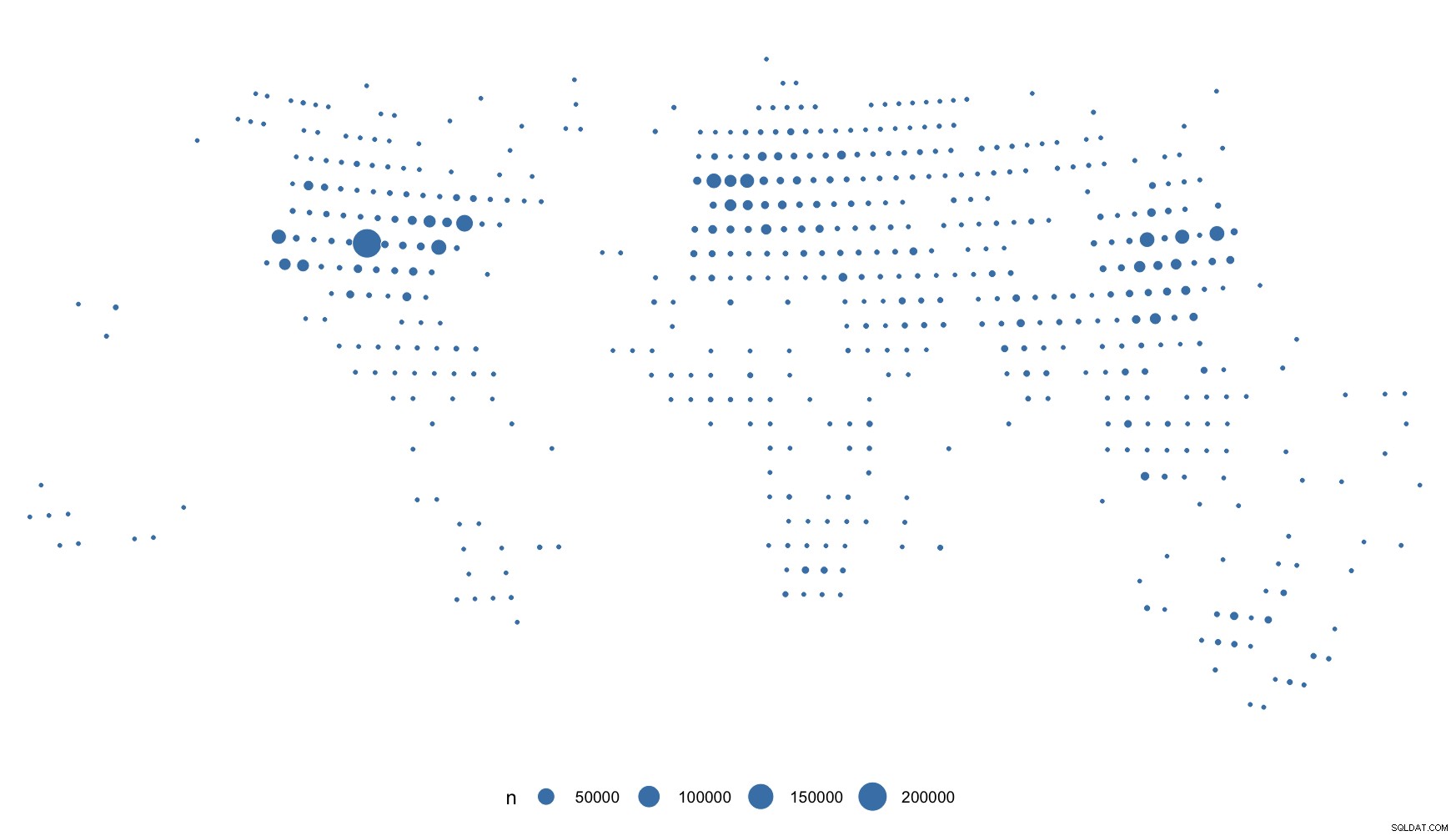
Wygenerujemy kilka adresów IP, zlokalizujemy je i wykreślimy:

library(iptools)
library(rgeolocate)
library(tidyverse)

Wygeneruj milion (zbyt równomiernie rozłożonych) losowych adresów IPv4:

ips <- ip_random(1000000)

I zlokalizuj je:

system.time(
  rgeolocate::maxmind(
    ips, "~/Data/GeoLite2-City.mmdb", c("longitude", "latitude")
  ) -> xdf
)
##    user  system elapsed 
##   5.016   0.131   5.217 

5s dla 1m IPv4.

Teraz, ze względu na jednolitość, bąbelki będą głupio małe, więc tylko w tym przykładzie zaokrąglimy je trochę w górę:

xdf %>% 
  mutate(
    longitude = (longitude %/% 5) * 5,
    latitude = (latitude %/% 5) * 5
  ) %>%  
  count(longitude, latitude) -> pts

I wykreśl je:

ggplot(pts) +
  geom_point(
    aes(longitude, latitude, size = n), 
    shape=21, fill = "steelblue", color = "white", stroke=0.25
  ) +
  ggalt::coord_proj("+proj=wintri") +
  ggthemes::theme_map() +
  theme(legend.justification = "center") +
  theme(legend.position = "bottom")

Możesz zobaczyć, co mam na myśli „zbyt jednolite”. Ale masz „prawdziwe” IPv4, więc powinieneś być gtg.

Rozważ użycie scale_size_area() , ale szczerze mówiąc, rozważ w ogóle nie kreślenie adresów IPv4 na mapie geograficznej. Zajmuję się badaniami na skalę internetową, a twierdzenia o dokładności pozostawiają wiele do życzenia. Z tego powodu rzadko schodzę poniżej atrybucji na poziomie kraju (a płacimy za „prawdziwe” dane).