Niedawno mój przyjaciel Erland Sommarskog przedstawił mi nowe wyzwanie wysp. Opiera się na pytaniu z forum publicznej bazy danych. Samo wyzwanie nie jest skomplikowane w przypadku korzystania z dobrze znanych technik, które wykorzystują przede wszystkim funkcje okien. Jednak te techniki wymagają jawnego sortowania pomimo obecności indeksu pomocniczego. Wpływa to na skalowalność i czas odpowiedzi rozwiązań. Lubię wyzwania, postanowiłem znaleźć rozwiązanie, aby zminimalizować liczbę wyraźnych operatorów sortowania w planie, lub jeszcze lepiej, całkowicie wyeliminować ich potrzebę. I znalazłem takie rozwiązanie.
Zacznę od przedstawienia uogólnionej formy wyzwania. Następnie pokażę dwa rozwiązania oparte na znanych technikach, a następnie nowe rozwiązanie. Na koniec porównam wydajność różnych rozwiązań.
Polecam spróbować znaleźć rozwiązanie przed wdrożeniem mojego.
Wyzwanie
Przedstawię uogólnioną formę oryginalnego wyzwania wysp Erlanda.
Użyj poniższego kodu, aby utworzyć tabelę o nazwie T1 i wypełnić ją małym zestawem przykładowych danych:
SET NOCOUNT ON;
USE tempdb;
DROP TABLE IF EXISTS dbo.T1
CREATE TABLE dbo.T1
(
grp VARCHAR(10) NOT NULL,
ord INT NOT NULL,
val VARCHAR(10) NOT NULL,
CONSTRAINT PK_T1 PRIMARY KEY(grp, ord)
);
GO
INSERT INTO dbo.T1(grp, ord, val) VALUES
('Group A', 1002, 'Y'),
('Group A', 1003, 'Y'),
('Group A', 1005, 'Y'),
('Group A', 1007, 'N'),
('Group A', 1011, 'N'),
('Group A', 1013, 'N'),
('Group A', 1017, 'Y'),
('Group A', 1019, 'Y'),
('Group A', 1023, 'N'),
('Group A', 1029, 'N'),
('Group B', 1001, 'X'),
('Group B', 1002, 'X'),
('Group B', 1003, 'Z'),
('Group B', 1005, 'Z'),
('Group B', 1008, 'Z'),
('Group B', 1013, 'Z'),
('Group B', 1021, 'Y'),
('Group B', 1034, 'Y'); Wyzwanie jest następujące:
Zakładając partycjonowanie w oparciu o kolumnę grp i kolejność w oparciu o porządek kolumny, oblicz kolejne numery wierszy zaczynające się od 1 w każdej kolejnej grupie wierszy o tej samej wartości w kolumnie val. Poniżej znajduje się pożądany wynik dla danego małego zestawu przykładowych danych:
grp ord val seqno -------- ----- ---- ------ Group A 1002 Y 1 Group A 1003 Y 2 Group A 1005 Y 3 Group A 1007 N 1 Group A 1011 N 2 Group A 1013 N 3 Group A 1017 Y 1 Group A 1019 Y 2 Group A 1023 N 1 Group A 1029 N 2 Group B 1001 X 1 Group B 1002 X 2 Group B 1003 Z 1 Group B 1005 Z 2 Group B 1008 Z 3 Group B 1013 Z 4 Group B 1021 Y 1 Group B 1034 Y 2
Zwróć uwagę na definicję ograniczenia klucza podstawowego na podstawie klucza złożonego (grp, ord), co powoduje powstanie indeksu klastrowego opartego na tym samym kluczu. Ten indeks może potencjalnie obsługiwać funkcje okna podzielone według grp i uporządkowane według ord.
Aby przetestować wydajność swojego rozwiązania, musisz wypełnić tabelę większą ilością przykładowych danych. Użyj następującego kodu, aby utworzyć funkcję pomocniczą GetNums:
CREATE FUNCTION dbo.GetNums(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums
ORDER BY rownum;
GO Użyj poniższego kodu, aby wypełnić T1, po zmianie parametrów reprezentujących liczbę grup, liczbę wierszy na grupę i liczbę odrębnych wartości, jak chcesz:
DECLARE
@numgroups AS INT = 1000,
@rowspergroup AS INT = 10000, -- test with 1000 to 10000 here
@uniquevalues AS INT = 5;
ALTER TABLE dbo.T1 DROP CONSTRAINT PK_T1;
TRUNCATE TABLE dbo.T1;
INSERT INTO dbo.T1 WITH(TABLOCK) (grp, ord, val)
SELECT
CAST(G.n AS VARCHAR(10)) AS grp,
CAST(R.n AS INT) AS ord,
CAST(ABS(CHECKSUM(NEWID())) % @uniquevalues + 1 AS VARCHAR(10)) AS val
FROM dbo.GetNums(1, @numgroups) AS G
CROSS JOIN dbo.GetNums(1, @rowspergroup) AS R;
ALTER TABLE dbo.T1 ADD CONSTRAINT PK_T1 PRIMARY KEY CLUSTERED(grp, ord);
W moich testach wydajności wypełniłem tabelę 1000 grup, od 1000 do 10 000 wierszy na grupę (czyli od 1 mln do 10 mln wierszy) i 5 różnymi wartościami. Użyłem SELECT INTO instrukcja do zapisania wyniku w tabeli tymczasowej.
Moja maszyna testowa ma cztery logiczne procesory z systemem SQL Server 2019 Enterprise.
Zakładam, że używasz środowiska zaprojektowanego do obsługi trybu wsadowego w magazynie wierszy bezpośrednio, np. przy użyciu wersji SQL Server 2019 Enterprise, takiej jak moja, lub pośrednio, tworząc w tabeli fikcyjny indeks magazynu kolumn.
Pamiętaj, dodatkowe punkty, jeśli uda Ci się wymyślić skuteczne rozwiązanie bez wyraźnego sortowania w planie. Powodzenia!
Czy operator sortowania jest potrzebny do optymalizacji funkcji okien?
Zanim omówię rozwiązania, trochę tła optymalizacji, więc to, co zobaczysz później w planach zapytań, będzie miało więcej sensu.
Najczęstsze techniki rozwiązywania zadań związanych z wyspami, takie jak nasze, obejmują użycie pewnej kombinacji funkcji okna agregującego i/lub rankingowego. SQL Server może przetwarzać takie funkcje okien przy użyciu serii starszych operatorów trybu wierszy (Segment, Sequence Project, Segment, Window Spool, Stream Aggregate) lub nowszego i zwykle bardziej wydajnego operatora Window Aggregate w trybie wsadowym.
W obu przypadkach operatorzy zajmujący się obliczaniem funkcji okna muszą pobrać dane uporządkowane przez elementy podziału i porządkowania okna. Jeśli nie masz indeksu pomocniczego, naturalnie SQL Server będzie musiał wprowadzić do planu operator Sort. Na przykład, jeśli masz wiele funkcji okien w swoim rozwiązaniu z więcej niż jedną unikalną kombinacją partycjonowania i porządkowania, na pewno masz w planie jawne sortowanie. Ale co, jeśli masz tylko jedną unikalną kombinację partycjonowania i porządkowania oraz indeks pomocniczy?
Starsza metoda trybu wiersza może polegać na zamówionych w przedsprzedaży danych pozyskiwanych z indeksu bez potrzeby jawnego operatora sortowania zarówno w trybie szeregowym, jak i równoległym. Nowszy operator trybu wsadowego eliminuje wiele nieefektywności starszej optymalizacji trybu wsadowego i ma nieodłączne zalety przetwarzania w trybie wsadowym. Jednak jego bieżąca implementacja równoległa wymaga pośredniczącego operatora sortowania równoległego w trybie wsadowym, nawet jeśli obecny jest indeks pomocniczy. Tylko jego szeregowa implementacja może polegać na kolejności indeksów bez operatora sortowania. To wszystko, co można powiedzieć, gdy optymalizator musi wybrać strategię do obsługi funkcji okna, zakładając, że masz indeks pomocniczy, będzie to generalnie jedna z następujących czterech opcji:
- Tryb rzędowy, szeregowy, bez sortowania
- Tryb rzędowy, równoległy, bez sortowania
- Tryb wsadowy, seryjny, bez sortowania
- Tryb wsadowy, równoległy, sortowanie
Niezależnie od tego, który z nich spowoduje najniższy koszt planu, zostanie wybrany, zakładając oczywiście, że spełnione są warunki wstępne dotyczące równoległości i trybu wsadowego. Zwykle, aby optymalizator uzasadniał plan równoległy, korzyści z równoległości muszą przewyższać dodatkową pracę, taką jak synchronizacja wątków. W przypadku opcji 4 powyżej korzyści z równoległości muszą przewyższać zwykłą dodatkową pracę związaną z równoległością oraz dodatkowe sortowanie.
Eksperymentując z różnymi rozwiązaniami naszego wyzwania, miałem przypadki, w których optymalizator wybrał opcję 2 powyżej. Wybrał ją pomimo faktu, że metoda trybu wierszowego wiąże się z kilkoma nieefektywnościami, ponieważ korzyści wynikające z równoległości i braku sortowania zaowocowały planem o niższym koszcie niż rozwiązania alternatywne. W niektórych przypadkach wymuszenie planu szeregowego z podpowiedzią skutkowało opcją 3 powyżej i lepszą wydajnością.
Mając to na uwadze, spójrzmy na rozwiązania. Zacznę od dwóch rozwiązań opartych na znanych technikach wykonywania zadań wyspowych, które nie mogą uniknąć wyraźnego sortowania w planie.
Rozwiązanie oparte na znanej technice 1
Poniżej znajduje się pierwsze rozwiązanie naszego wyzwania, które opiera się na znanej od jakiegoś czasu technice:
WITH C AS
(
SELECT *,
ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) -
ROW_NUMBER() OVER(PARTITION BY grp, val ORDER BY ord) AS island
FROM dbo.T1
)
SELECT grp, ord, val,
ROW_NUMBER() OVER(PARTITION BY grp, val, island ORDER BY ord) AS seqno
FROM C; Nazywam to znanym rozwiązaniem 1.
CTE o nazwie C opiera się na zapytaniu, które oblicza dwa numery wierszy. Pierwszy (nazywam się rn1) jest podzielony na partycje przez grp i uporządkowany według ord. Drugi (nazywam się rn2) jest podzielony na partycje grp i val i uporządkowany według ord. Ponieważ rn1 ma przerwy między różnymi grupami tej samej wartości, a rn2 nie, różnica między rn1 i rn2 (kolumna zwana wyspą) jest unikalną stałą wartością dla wszystkich wierszy z tymi samymi wartościami grp i val. Poniżej znajduje się wynik zapytania wewnętrznego, w tym wyniki obliczeń liczby dwóch wierszy, które nie są zwracane jako oddzielne kolumny:
grp ord val rn1 rn2 island -------- ----- ---- ---- ---- ------- Group A 1002 Y 1 1 0 Group A 1003 Y 2 2 0 Group A 1005 Y 3 3 0 Group A 1007 N 4 1 3 Group A 1011 N 5 2 3 Group A 1013 N 6 3 3 Group A 1017 Y 7 4 3 Group A 1019 Y 8 5 3 Group A 1023 N 9 4 5 Group A 1029 N 10 5 5 Group B 1001 X 1 1 0 Group B 1002 X 2 2 0 Group B 1003 Z 3 1 2 Group B 1005 Z 4 2 2 Group B 1008 Z 5 3 2 Group B 1013 Z 6 4 2 Group B 1021 Y 7 1 6 Group B 1034 Y 8 2 6
To, co pozostało do wykonania w zewnętrznym zapytaniu, to obliczenie kolejnego kolumny wyników przy użyciu funkcji ROW_NUMBER, podzielonej na partycje grp, val i island oraz uporządkowanej według ord, generując pożądany wynik.
Zauważ, że możesz uzyskać tę samą wartość wyspy dla różnych wartości val w tej samej partycji, tak jak na powyższym wyjściu. Dlatego ważne jest, aby używać grp, val i island jako elementów partycjonujących okna, a nie samych grp i island.
Podobnie, jeśli masz do czynienia z zadaniem wysp, które wymaga pogrupowania danych według wyspy i obliczenia agregacji grup, możesz pogrupować wiersze według grp, val i island. Ale tak nie jest w przypadku naszego wyzwania. Tutaj miałeś za zadanie po prostu obliczyć numery wierszy niezależnie dla każdej wyspy.
Rysunek 1 przedstawia domyślny plan, który otrzymałem dla tego rozwiązania na moim komputerze po zapełnieniu tabeli 10 milionami wierszy.
Rysunek 1:Plan równoległy dla znanego rozwiązania 1
Obliczenie rn1 może opierać się na kolejności indeksów. Tak więc optymalizator wybrał dla tego strategię bez sortowania + tryb równoległych wierszy (pierwsze operatory segmentu i projektu sekwencji w planie). Ponieważ obliczenia zarówno rn2, jak i seqno wykorzystują własne unikalne kombinacje elementów partycjonowania i porządkowania, jawne sortowanie jest nieuniknione dla tych, niezależnie od zastosowanej strategii. Tak więc optymalizator wybrał strategię sort + równoległy tryb wsadowy dla obu. Ten plan obejmuje dwa wyraźne operatory sortowania.
W moim teście wydajności rozwiązanie to zajęło 3,68 sekundy, aby ukończyć 1 mln wierszy i 43,1 sekundy względem 10 mln wierszy.
Jak wspomniałem, testowałem wszystkie rozwiązania również wymuszając plan szeregowy (z podpowiedzią MAXDOP 1). Plan szeregowy dla tego rozwiązania pokazano na rysunku 1.
Rysunek 2:Plan szeregowy dla znanego rozwiązania 1
Zgodnie z oczekiwaniami, tym razem również obliczenie rn1 wykorzystuje strategię trybu wsadowego bez poprzedzającego operatora sortowania, ale plan nadal ma dwa operatory sortowania dla kolejnych obliczeń numerów wierszy. Plan szeregowy działał gorzej niż równoległy na moim komputerze ze wszystkimi testowanymi rozmiarami danych wejściowych, zabierając 4,54 sekundy na ukończenie z 1 mln wierszy i 61,5 sekundy z 10 mln wierszy.
Rozwiązanie oparte na znanej technice 2
Drugie rozwiązanie, które przedstawię, opiera się na genialnej technice wykrywania wysp, której nauczyłem się od Paula White'a kilka lat temu. Poniżej znajduje się kompletny kod rozwiązania oparty na tej technice:
WITH C1 AS
(
SELECT *,
CASE
WHEN val = LAG(val) OVER(PARTITION BY grp ORDER BY ord) THEN 0
ELSE 1
END AS isstart
FROM dbo.T1
),
C2 AS
(
SELECT *,
SUM(isstart) OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS island
FROM C1
)
SELECT grp, ord, val,
ROW_NUMBER() OVER(PARTITION BY grp, island ORDER BY ord) AS seqno
FROM C2; Będę nazywał to rozwiązanie znanym rozwiązaniem 2.
Zapytanie definiujące obliczenia CTE C1 używa wyrażenia CASE i funkcji okna LAG (podzielonej przez grp i uporządkowanej według ord) do obliczenia kolumny wyników o nazwie isstart. Ta kolumna ma wartość 0, gdy bieżąca wartość val jest taka sama jak poprzednia, a 1 w przeciwnym razie. Innymi słowy, jest to 1, gdy rząd jest pierwszym na wyspie, a 0 w przeciwnym razie.
Poniżej znajduje się wynik zapytania definiującego C1:
grp ord val isstart -------- ----- ---- -------- Group A 1002 Y 1 Group A 1003 Y 0 Group A 1005 Y 0 Group A 1007 N 1 Group A 1011 N 0 Group A 1013 N 0 Group A 1017 Y 1 Group A 1019 Y 0 Group A 1023 N 1 Group A 1029 N 0 Group B 1001 X 1 Group B 1002 X 0 Group B 1003 Z 1 Group B 1005 Z 0 Group B 1008 Z 0 Group B 1013 Z 0 Group B 1021 Y 1 Group B 1034 Y 0
Magia, jeśli chodzi o wykrywanie wysp, ma miejsce w CTE C2. Kwerenda definiująca je oblicza identyfikator wyspy za pomocą funkcji okna SUMA (również podzielonej na partycje przez grp i uporządkowanej według ord) zastosowanej do kolumny isstart. Kolumna wynikowa z identyfikatorem wyspy nazywa się wyspą. W każdej partycji otrzymujesz 1 za pierwszą wyspę, 2 za drugą i tak dalej. Tak więc kombinacja kolumn grp i wyspa jest identyfikatorem wyspy, którego można używać w zadaniach związanych z wyspami, które obejmują grupowanie według wyspy, gdy jest to istotne.
Poniżej znajduje się wynik zapytania definiującego C2:
grp ord val isstart island -------- ----- ---- -------- ------- Group A 1002 Y 1 1 Group A 1003 Y 0 1 Group A 1005 Y 0 1 Group A 1007 N 1 2 Group A 1011 N 0 2 Group A 1013 N 0 2 Group A 1017 Y 1 3 Group A 1019 Y 0 3 Group A 1023 N 1 4 Group A 1029 N 0 4 Group B 1001 X 1 1 Group B 1002 X 0 1 Group B 1003 Z 1 2 Group B 1005 Z 0 2 Group B 1008 Z 0 2 Group B 1013 Z 0 2 Group B 1021 Y 1 3 Group B 1034 Y 0 3
Na koniec zapytanie zewnętrzne oblicza żądaną kolumnę wyników seqno z funkcją ROW_NUMBER, podzieloną na partycje grp i island oraz uporządkowaną według ord. Zauważ, że ta kombinacja partycjonowania i porządkowania elementów różni się od tej używanej przez poprzednie funkcje okna. Podczas gdy obliczenia pierwszych dwóch funkcji okna mogą potencjalnie polegać na kolejności indeksów, ostatnia nie może.
Rysunek 3 przedstawia domyślny plan, który otrzymałem dla tego rozwiązania.
Rysunek 3:Plan równoległy dla znanego rozwiązania 2
Jak widać na planie, obliczenia pierwszych dwóch funkcji okna wykorzystują strategię bez sortowania + tryb równoległych wierszy, a obliczenia ostatniej używają strategii sortowania + równoległego trybu wsadowego.
Czasy działania, jakie uzyskałem dla tego rozwiązania, wahały się od 2,57 sekundy w stosunku do 1 mln wierszy do 46,2 sekundy w przypadku 10 mln wierszy.
Kiedy wymuszam przetwarzanie seryjne, otrzymałem plan pokazany na rysunku 4.
Rysunek 4:Plan szeregowy dla znanego rozwiązania 2
Zgodnie z oczekiwaniami, tym razem wszystkie obliczenia funkcji okna opierają się na strategii trybu wsadowego. Pierwsze dwa bez wcześniejszego sortowania, a ostatnie z. Zarówno plan równoległy, jak i szeregowy obejmowały jednego jawnego operatora sortowania. Plan szeregowy działał lepiej niż plan równoległy na moim komputerze z testowanymi rozmiarami wejściowymi. Czasy działania, które uzyskałem dla wymuszonego planu szeregowego, wahały się od 1,75 sekundy w przypadku 1 mln wierszy do 21,7 sekundy w przypadku 10 mln wierszy.
Rozwiązanie oparte na nowej technice
Kiedy Erland przedstawił to wyzwanie na prywatnym forum, ludzie byli sceptycznie nastawieni do możliwości rozwiązania go za pomocą zapytania, które zostało zoptymalizowane za pomocą planu bez jawnego sortowania. To wszystko, co musiałem usłyszeć, aby mnie zmotywować. Oto, co wymyśliłem:
WITH C1 AS
(
SELECT *,
ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) AS rn,
LAG(val) OVER(PARTITION BY grp ORDER BY ord) AS prev
FROM dbo.T1
),
C2 AS
(
SELECT *,
MAX(CASE WHEN val = prev THEN NULL ELSE rn END)
OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS firstrn
FROM C1
)
SELECT grp, ord, val, rn - firstrn + 1 AS seqno
FROM C2; Rozwiązanie wykorzystuje trzy funkcje okna:LAG, ROW_NUMBER i MAX. Ważną rzeczą tutaj jest to, że wszystkie trzy opierają się na partycjonowaniu grp i kolejności zamówień, która jest dostosowana do pomocniczej kolejności kluczy indeksu.
Zapytanie definiujące CTE C1 używa funkcji ROW_NUMBER do obliczenia numerów wierszy (kolumna rn) oraz funkcji LAG do zwrócenia poprzedniej wartości val (prev column).
Oto wynik zapytania definiującego C1:
grp ord val rn prev -------- ----- ---- --- ----- Group A 1002 Y 1 NULL Group A 1003 Y 2 Y Group A 1005 Y 3 Y Group A 1007 N 4 Y Group A 1011 N 5 N Group A 1013 N 6 N Group A 1017 Y 7 N Group A 1019 Y 8 Y Group A 1023 N 9 Y Group A 1029 N 10 N Group B 1001 X 1 NULL Group B 1002 X 2 X Group B 1003 Z 3 X Group B 1005 Z 4 Z Group B 1008 Z 5 Z Group B 1013 Z 6 Z Group B 1021 Y 7 Z Group B 1034 Y 8 Y
Zauważ, że kiedy val i prev są takie same, nie jest to pierwszy rząd na wyspie, w przeciwnym razie tak jest.
W oparciu o tę logikę zapytanie definiujące CTE C2 używa wyrażenia CASE, które zwraca rn, gdy wiersz jest pierwszym na wyspie, a NULL w przeciwnym razie. Kod następnie stosuje funkcję okna MAX do wyniku wyrażenia CASE, zwracając pierwszy rn wyspy (pierwsza kolumna).
Oto wynik zapytania definiującego C2, w tym wynik wyrażenia CASE:
grp ord val rn prev CASE firstrn -------- ----- ---- --- ----- ----- -------- Group A 1002 Y 1 NULL 1 1 Group A 1003 Y 2 Y NULL 1 Group A 1005 Y 3 Y NULL 1 Group A 1007 N 4 Y 4 4 Group A 1011 N 5 N NULL 4 Group A 1013 N 6 N NULL 4 Group A 1017 Y 7 N 7 7 Group A 1019 Y 8 Y NULL 7 Group A 1023 N 9 Y 9 9 Group A 1029 N 10 N NULL 9 Group B 1001 X 1 NULL 1 1 Group B 1002 X 2 X NULL 1 Group B 1003 Z 3 X 3 3 Group B 1005 Z 4 Z NULL 3 Group B 1008 Z 5 Z NULL 3 Group B 1013 Z 6 Z NULL 3 Group B 1021 Y 7 Z 7 7 Group B 1034 Y 8 Y NULL 7
To, co pozostało do zewnętrznego zapytania, to obliczenie żądanego wyniku kolumny seqno jako rn minus firstrn plus 1.
Rysunek 5 przedstawia domyślny plan równoległy, który otrzymałem dla tego rozwiązania podczas testowania go za pomocą instrukcji SELECT INTO, zapisując wynik do tabeli tymczasowej.
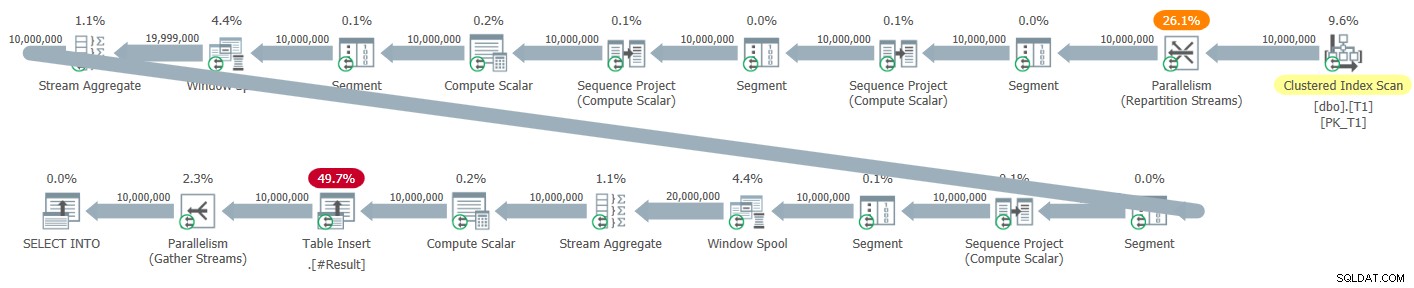Rysunek 5:Plan równoległy dla nowego rozwiązania
W tym planie nie ma wyraźnych operatorów sortowania. Jednak wszystkie trzy funkcje okna są obliczane przy użyciu strategii bez sortowania + trybu wierszy równoległych, więc brakuje nam korzyści z przetwarzania wsadowego. Czasy działania, które otrzymałem dla tego rozwiązania w planie równoległym, wynosiły od 2,47 sekundy do 1 mln wierszy i 41,4 do 10 mln wierszy.
Tutaj istnieje duże prawdopodobieństwo, że plan szeregowy z przetwarzaniem wsadowym będzie działał znacznie lepiej, zwłaszcza gdy maszyna nie ma wielu procesorów. Przypomnijmy, że testuję swoje rozwiązania na maszynie z 4 logicznymi procesorami. Rysunek 6 przedstawia plan, jaki otrzymałem dla tego rozwiązania, gdy wymuszam przetwarzanie szeregowe.
Rysunek 6:Plan seryjny dla nowego rozwiązania
Wszystkie trzy funkcje okna wykorzystują strategię trybu wsadowego bez sortowania + szeregowego. A wyniki są imponujące. Czas działania tego rozwiązania wahał się od 0,5 sekundy do 1 mln rzędów i 5,49 sekundy do 10 mln rzędów. Ciekawe jest również to, że podczas testowania go jako zwykłej instrukcji SELECT (z odrzuconymi wynikami) w przeciwieństwie do instrukcji SELECT INTO, SQL Server domyślnie wybrał plan szeregowy. W przypadku pozostałych dwóch rozwiązań domyślnie otrzymałem plan równoległy zarówno z SELECT, jak i SELECT INTO.
Zobacz następną sekcję, aby uzyskać pełne wyniki testu wydajności.
Porównanie wydajności
Oto kod, którego użyłem do przetestowania trzech rozwiązań, oczywiście odkomentowując wskazówkę MAXDOP 1, aby przetestować plany szeregowe:
-- Test Known Solution 1
DROP TABLE IF EXISTS #Result;
WITH C AS
(
SELECT *,
ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) -
ROW_NUMBER() OVER(PARTITION BY grp, val ORDER BY ord) AS island
FROM dbo.T1
)
SELECT grp, ord, val,
ROW_NUMBER() OVER(PARTITION BY grp, val, island ORDER BY ord) AS seqno
INTO #Result
FROM C
/* OPTION(MAXDOP 1) */; -- uncomment for serial test
GO
-- Test Known Solution 2
DROP TABLE IF EXISTS #Result;
WITH C1 AS
(
SELECT *,
CASE
WHEN val = LAG(val) OVER(PARTITION BY grp ORDER BY ord) THEN 0
ELSE 1
END AS isstart
FROM dbo.T1
),
C2 AS
(
SELECT *,
SUM(isstart) OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS island
FROM C1
)
SELECT grp, ord, val,
ROW_NUMBER() OVER(PARTITION BY grp, island ORDER BY ord) AS seqno
INTO #Result
FROM C2
/* OPTION(MAXDOP 1) */;
GO
-- Test New Solution
DROP TABLE IF EXISTS #Result;
WITH C1 AS
(
SELECT *,
ROW_NUMBER() OVER(PARTITION BY grp ORDER BY ord) AS rn,
LAG(val) OVER(PARTITION BY grp ORDER BY ord) AS prev
FROM dbo.T1
),
C2 AS
(
SELECT *,
MAX(CASE WHEN val = prev THEN NULL ELSE rn END)
OVER(PARTITION BY grp ORDER BY ord ROWS UNBOUNDED PRECEDING) AS firstrn
FROM C1
)
SELECT grp, ord, val, rn - firstrn + 1 AS seqno
INTO #Result
FROM C2
/* OPTION(MAXDOP 1) */; Rysunek 7 przedstawia czasy wykonywania zarówno planów równoległych, jak i szeregowych dla wszystkich rozwiązań w odniesieniu do różnych rozmiarów danych wejściowych.
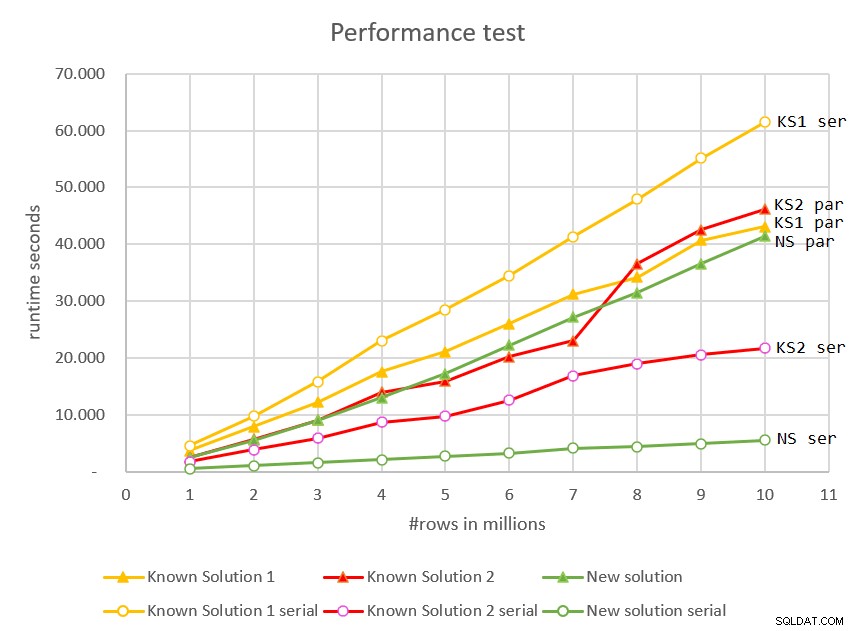Rysunek 7:Porównanie wydajności
Wyraźnym zwycięzcą jest nowe rozwiązanie, wykorzystujące tryb szeregowy. Ma świetną wydajność, liniowe skalowanie i natychmiastowy czas reakcji.
Wniosek
Zadania na wyspach są dość powszechne w prawdziwym życiu. Wiele z nich obejmuje zarówno identyfikację wysp, jak i grupowanie danych według wysp. Wyzwanie wysp Erlanda, na którym skupiliśmy się w tym artykule, jest nieco bardziej wyjątkowe, ponieważ nie obejmuje grupowania, ale zamiast tego sekwencjonowanie rzędów każdej wyspy z numerami rzędów.
Przedstawiłem dwa rozwiązania oparte na znanych technikach identyfikacji wysp. Problem z obydwoma polega na tym, że skutkują one planami obejmującymi jawne sortowanie, co negatywnie wpływa na wydajność, skalowalność i czas odpowiedzi rozwiązań. Przedstawiłem też nową technikę, która zaowocowała planem bez sortowania. Plan szeregowy dla tego rozwiązania, który wykorzystuje strategię bez sortowania + szeregowy tryb wsadowy, charakteryzuje się doskonałą wydajnością, skalowaniem liniowym i natychmiastowym czasem reakcji. To niefortunne, przynajmniej na razie, nie możemy mieć strategii bez sortowania + równoległego trybu wsadowego do obsługi funkcji okien.
