Rozumiem, że nie ma rozszerzenia, które to robi, więc znalazłem ograniczone obejście:
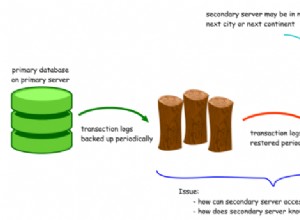
Jeśli A i B są znormalizowane (długość 1), cos(A, B) = 1 - 0.5 * ||A - B||^2 . ||A - B|| to odległość euklidesowa, a cos(A, B) jest podobieństwo cosinus. Zatem większa odległość euklidesowa <=> mniejsze podobieństwo cosinusów (ma sens intuicyjnie, jeśli wyobrazisz sobie okrąg jednostkowy), a jeśli masz wektory inne niż normalne, zmiana ich wielkości bez zmiany ich kierunku nie wpływa na ich podobieństwa cosinusów. Świetnie, więc mogę znormalizować moje wektory i porównać ich odległości euklidesowe...
Jest ładna odpowiedź tutaj o kostce , który obsługuje n-wymiarowe punkty i indeksy GiST na euklidesowych odległość, ale obsługuje tylko 100 lub mniej wymiarów (można zhakować wyżej, ale miałem problemy około 135 i więcej, więc teraz się obawiam). Wymaga również Postgresa 9.6 lub nowszego.
A więc:
- Upewnij się, że nie obchodzi mnie posiadanie co najwyżej 100 wymiarów. Uaktualnij do Postgresa 9.6 lub nowszego.
- Wypełnij moją tabelę tablicami reprezentującymi wektory.
- Znormalizuj wektory, aby utworzyć dodatkową kolumnę
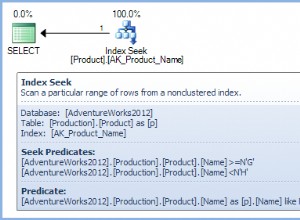
cubezwrotnica. Utwórz indeks GiST w tej kolumnie. - Uporządkuj według odległości euklidesowej rosnąco, aby uzyskać podobieństwo cosinusów malejąco:
EXPLAIN SELECT * FROM mytable ORDER BY normalized <-> cube(array[1,2,3,4,5,6,7,8,9,0]) LIMIT 10;
Jeśli potrzebuję więcej niż 100 wymiarów, być może uda mi się to osiągnąć za pomocą wielu indeksowanych kolumn. W takim przypadku zaktualizuje odpowiedź.
Aktualizacja: Jestem prawie pewien, że nie mogę nic zrobić z dzieleniem wektora> 100-wymiarowego na wiele kolumn. W końcu muszę zeskanować cały stół.