Powracające kombinacje
Używając tabeli liczb lub CTE generującego liczby, wybierz od 0 do 2^n - 1. Używając pozycji bitowych zawierających jedynki w tych liczbach, aby wskazać obecność lub nieobecność elementów względnych w kombinacji i eliminując te, które nie mają poprawną liczbę wartości, powinieneś być w stanie zwrócić zestaw wyników ze wszystkimi pożądanymi kombinacjami.
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
To zapytanie działa całkiem nieźle, ale pomyślałem o sposobie jego optymalizacji, korzystając z Sprawna liczba bitów równoległych aby najpierw uzyskać odpowiednią liczbę przedmiotów pobieranych jednocześnie. Działa to od 3 do 3,5 razy szybciej (zarówno procesor, jak i czas):
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
Poszedłem i przeczytałem stronę o liczeniu bitów i pomyślałem, że może to działać lepiej, jeśli nie zrobię % 255, ale zajmę się arytmetyką bitową. Kiedy będę miał okazję, spróbuję tego i zobaczę, jak się układa.
Moje oświadczenia dotyczące wydajności są oparte na zapytaniach uruchamianych bez klauzuli ORDER BY. Dla jasności, to, co ten kod robi, to zliczanie liczby zestawów 1-bitów w Num z Numbers stół. Dzieje się tak, ponieważ liczba jest używana jako rodzaj indeksatora do wyboru, które elementy zestawu znajdują się w bieżącej kombinacji, więc liczba 1-bitów będzie taka sama.
Mam nadzieję, że Ci się spodoba!
Dla przypomnienia, ta technika używania bitowego wzorca liczb całkowitych do wybierania elementów zbioru jest tym, co ukułem jako „Vertical Cross Join”. Skutecznie skutkuje połączeniem krzyżowym wielu zestawów danych, gdzie liczba zestawów i złączeń krzyżowych jest dowolna. Tutaj liczba zestawów to liczba elementów pobranych na raz.
Właściwie łączenie krzyżowe w zwykłym sensie poziomym (dodawanie kolejnych kolumn do istniejącej listy kolumn przy każdym łączeniu) wyglądałoby mniej więcej tak:
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
Moje zapytania powyżej skutecznie "połączenia krzyżowe" tyle razy, ile to konieczne, przy tylko jednym sprzężeniu. Oczywiście wyniki są niezmienne w porównaniu z rzeczywistymi połączeniami krzyżowymi, ale to drobna sprawa.
Krytyka Twojego kodu
Po pierwsze, czy mogę zasugerować tę zmianę w twoim Factorial UDF:
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
Teraz możesz obliczyć znacznie większe zestawy kombinacji, a dodatkowo jest to wydajniejsze. Możesz nawet rozważyć użycie decimal(38, 0) aby umożliwić większe obliczenia pośrednie w obliczeniach kombinacji.
Po drugie, podane zapytanie nie zwraca poprawnych wyników. Na przykład, używając moich danych testowych z poniższych testów wydajności, zestaw 1 jest taki sam jak zestaw 18. Wygląda na to, że twoje zapytanie ma przesuwający się pasek, który owija się wokół:każdy zestaw ma zawsze 5 sąsiednich elementów, wygląda mniej więcej tak (obróciłem się aby było łatwiej zobaczyć):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
Porównaj wzór z moich zapytań:
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
Aby wskazać wszystkim zainteresowanym wzór bitowy -> indeks kombinacji, zauważ, że 31 w systemie binarnym =11111, a wzorzec to ABCDE. 121 w formacie binarnym to 1111001, a wzorzec to A__DEFG (zmapowany wstecz).
Wyniki wydajności z tabelą liczb rzeczywistych
Przeprowadziłem kilka testów wydajności z dużymi zestawami w moim drugim zapytaniu powyżej. W tej chwili nie mam zapisu używanej wersji serwera. Oto moje dane testowe:
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
Peter pokazał, że to „vertical cross join” nie działa tak dobrze, jak proste pisanie dynamicznego SQL, aby faktycznie wykonać CROSS JOIN, którego unika. Kosztem kilku dodatkowych odczytów jego rozwiązanie ma metryki od 10 do 17 razy lepsze. Wydajność jego zapytania spada szybciej niż moje wraz ze wzrostem nakładu pracy, ale nie na tyle szybko, aby powstrzymać kogokolwiek przed jego użyciem.
Drugi zestaw liczb poniżej to czynnik podzielony przez pierwszy wiersz w tabeli, aby pokazać, jak się skaluje.
Eryk
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
Piotr
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
Ekstrapolując, w końcu moje zapytanie będzie tańsze (choć od początku jest w odczytach), ale nie na długo. Aby użyć 21 pozycji w zestawie, wymagana jest tabela liczb sięgająca 2097152...
Oto komentarz, który pierwotnie zrobiłem, zanim zdałem sobie sprawę, że moje rozwiązanie będzie działać znacznie lepiej z tabelą liczb w locie:
Wyniki wydajności z tabelą liczb w locie
Kiedy pierwotnie napisałem tę odpowiedź, powiedziałem:
Cóż, spróbowałem i okazało się, że działa znacznie lepiej! Oto zapytanie, którego użyłem:
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
Zauważ, że wybrałem wartości na zmienne, aby skrócić czas i pamięć potrzebną do przetestowania wszystkiego. Serwer nadal wykonuje tę samą pracę. Zmodyfikowałem wersję Petera, aby była podobna, i usunęłam niepotrzebne dodatki, aby obie były tak szczupłe, jak to tylko możliwe. Wersja serwera używana do tych testów to Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) działa na maszynie wirtualnej.
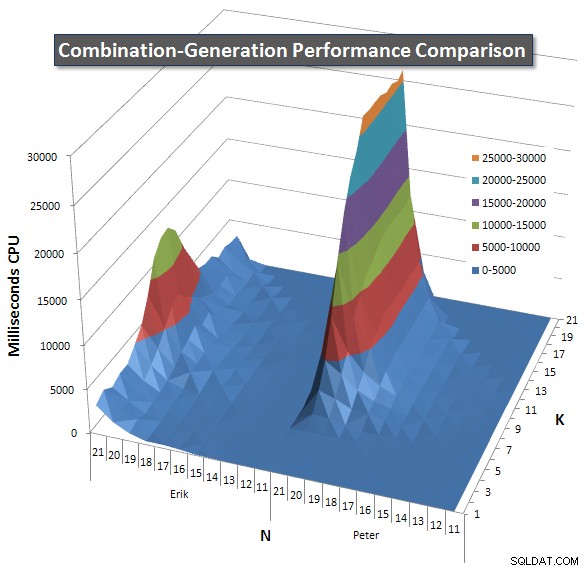
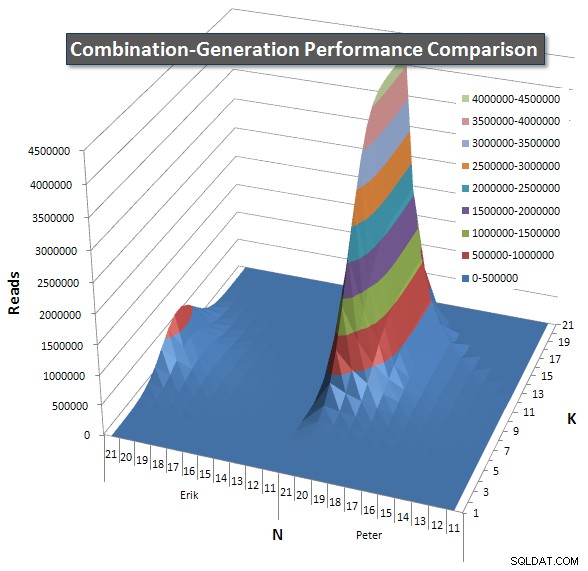
Poniżej znajdują się wykresy przedstawiające krzywe wydajności dla wartości N i K do 21. Dane bazowe dla nich znajdują się w inna odpowiedź na tej stronie . Wartości są wynikiem 5 uruchomień każdego zapytania dla każdej wartości K i N, a następnie odrzucenia najlepszych i najgorszych wartości dla każdej metryki i uśrednienia pozostałych 3.
Zasadniczo moja wersja ma „ramię” (w lewym rogu wykresu) przy wysokich wartościach N i niskich wartościach K, które powodują, że działa tam gorzej niż dynamiczna wersja SQL. Jednak pozostaje to dość niskie i stałe, a centralna wartość szczytowa wokół N =21 i K =11 jest znacznie niższa dla czasu trwania, procesora i odczytów niż w przypadku dynamicznej wersji SQL.
Dołączyłem wykres liczby wierszy, które każdy element ma zwrócić, dzięki czemu możesz zobaczyć, jak działa zapytanie w zestawieniu z tym, jak duże zadanie ma do wykonania.
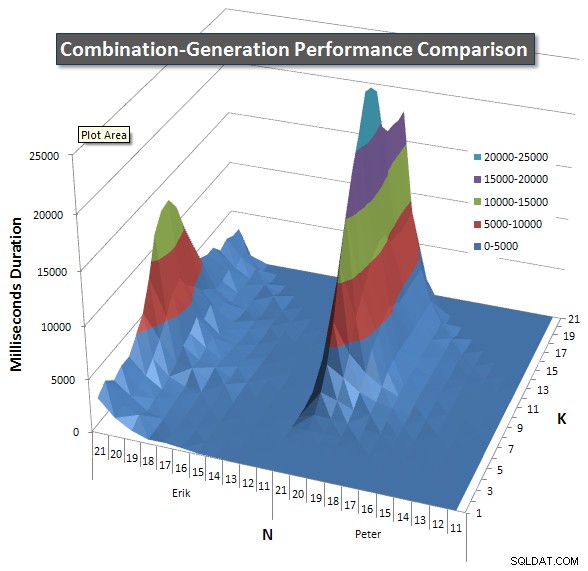
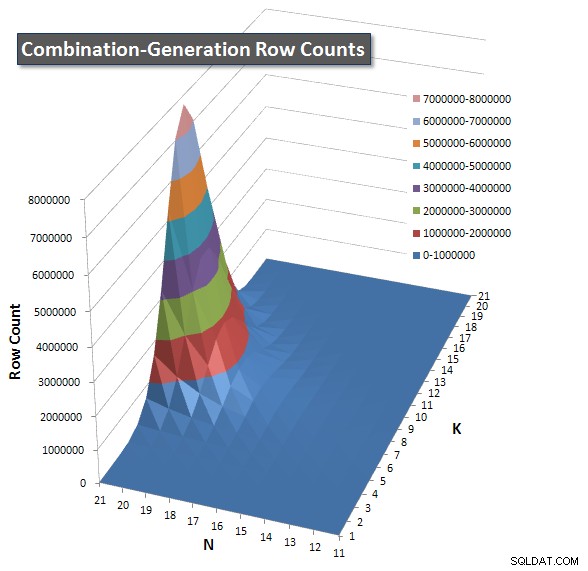
Zobacz moją dodatkową odpowiedź na tej stronie dla pełnych wyników wydajności. Osiągnąłem limit znaków postu i nie mogłem go tutaj uwzględnić. (Jakieś pomysły, gdzie jeszcze to umieścić?) Aby spojrzeć z innej perspektywy na wyniki wydajności mojej pierwszej wersji, oto ten sam format, co poprzednio:
Eryk
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
Piotr
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
Wnioski
- Tabele liczb w locie są lepsze niż prawdziwa tabela zawierająca wiersze, ponieważ odczytywanie jednej z dużej liczby wierszy wymaga dużej ilości operacji we/wy. Lepiej jest użyć trochę procesora.
- Moje wstępne testy nie były wystarczająco szerokie, aby naprawdę pokazać charakterystykę wydajności obu wersji.
- Wersję Petera można ulepszyć, sprawiając, że każdy JOIN nie tylko będzie większy niż poprzedni element, ale także ograniczy maksymalną wartość w oparciu o liczbę elementów, które należy zmieścić w zestawie. Na przykład przy 21 pozycjach pobranych jednorazowo jest tylko jedna odpowiedź z 21 wierszy (wszystkie 21 pozycji, jeden raz), ale pośrednie zestawy wierszy w wersji dynamicznego SQL, na początku planu wykonania, zawierają kombinacje takie jak " AU” w kroku 2, nawet jeśli zostanie odrzucone przy następnym łączeniu, ponieważ nie ma dostępnej wartości wyższej niż „U”. Podobnie pośredni zestaw wierszy w kroku 5 będzie zawierał „ARSTU”, ale jedyną prawidłową kombinacją w tym momencie jest „ABCDE”. Ta ulepszona wersja nie miałaby niższego szczytu w centrum, więc prawdopodobnie nie poprawiłaby go na tyle, aby stać się wyraźnym zwycięzcą, ale przynajmniej stałaby się symetryczna, aby wykresy nie pozostały maksymalne poza środkiem regionu, ale cofnęłyby się do blisko 0, jak moja wersja (patrz górny róg szczytów dla każdego zapytania).
Analiza czasu trwania
- Nie ma naprawdę znaczącej różnicy między wersjami w czasie trwania (>100 ms), dopóki 14 elementów nie zostanie pobranych po 12 naraz. Do tego momentu moja wersja wygrywa 30 razy, a dynamiczna wersja SQL wygrywa 43 razy.
- Począwszy od 14•12, moja wersja była szybsza 65 razy (59>100ms), a dynamiczna wersja SQL 64 razy (60>100ms). Jednak za każdym razem moja wersja była szybsza, oszczędzała łączny uśredniony czas trwania 256,5 sekundy, a gdy dynamiczna wersja SQL była szybsza, oszczędzała 80,2 sekundy.
- Całkowity średni czas trwania wszystkich prób wyniósł Erik 270,3 sekundy, Peter 446,2 sekundy.
- Jeżeli tabela przeglądowa została utworzona w celu określenia, której wersji użyć (wybierając szybszą dla danych wejściowych), wszystkie wyniki można wykonać w ciągu 188,7 sekundy. Użycie najwolniejszego za każdym razem zajęłoby 527,7 sekundy.
Analiza odczytów
Analiza czasu trwania wykazała, że moje zapytanie wygrało znaczną, ale niezbyt dużą kwotą. Po przełączeniu metryki na odczyty wyłania się zupełnie inny obraz — moje zapytanie wykorzystuje średnio 1/10 odczytów.
- Nie ma naprawdę znaczącej różnicy między wersjami w odczytach (>1000), dopóki 9 pozycji nie bierze 9 na raz. Do tego momentu moja wersja wygrywa 30 razy, a dynamiczna wersja SQL wygrywa 17 razy.
- Począwszy od 9•9, moja wersja używała mniej odczytów 118 razy (113>1000), a dynamiczna wersja SQL 69 razy (31>1000). Jednak za każdym razem moja wersja używała mniej odczytów, zapisywała średnio 75,9 mln odczytów, a gdy dynamiczna wersja SQL była szybsza, zapisywała 380 tys. odczytów.
- Łączna średnia odczytów dla wszystkich prób wyniosła Erik 8,4 mln, Peter 84 mln.
- Jeżeli tabela przeglądowa została utworzona w celu określenia, której wersji użyć (wybierając najlepszą dla danych wejściowych), wszystkie wyniki mogą być wykonane w 8M odczytach. Użycie najgorszego za każdym razem wymagałoby 84,3 mln odczytów.
Byłbym bardzo zainteresowany, aby zobaczyć wyniki zaktualizowanej dynamicznej wersji SQL, która nakłada dodatkowy górny limit na elementy wybrane na każdym kroku, jak opisano powyżej.
Uzupełnienie
Poniższa wersja mojego zapytania osiąga poprawę o około 2,25% w stosunku do wyników wydajności wymienionych powyżej. Użyłem metody liczenia bitów MIT HAKMEM i dodałem Convert(int) w wyniku row_number() ponieważ zwraca bigint. Oczywiście żałuję, że nie jest to wersja, której używałem do wszystkich testów wydajności, wykresów i danych powyżej, ale jest mało prawdopodobne, abym kiedykolwiek ją przerobił, ponieważ było to pracochłonne.
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
I nie mogłem się powstrzymać przed pokazaniem jeszcze jednej wersji, która wykonuje wyszukiwanie, aby uzyskać liczbę bitów. Może być nawet szybszy niż inne wersje:
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))