Dopasowanie podaży do popytu — rozwiązania, część 2

[ Skocz do:Oryginalne wyzwanie | Rozwiązania:Część 1 | Część 2 | Część 3 ]

W tym artykule kontynuuję omówienie rozwiązań dotyczących kuszącego dopasowania podaży do popytu, zaproponowanego przez Petera Larssona. Jeszcze raz dziękuję Luce, Kamilowi Kosno, Danielowi Brownowi, Brianowi Walkerowi, Joe Obbishowi, Rainerowi Hoffmannowi, Paulowi White'owi, Charliemu i Peterowi Larssonowi za przesłanie swoich rozwiązań.

W zeszłym miesiącu omówiłem rozwiązanie oparte na przecięciach przedziałów, używając klasycznego testu przecięcia przedziałów opartego na predykatach. Nazywam to rozwiązaniem klasycznymi skrzyżowaniami . Klasyczne podejście do przecięć interwałów skutkuje planem ze skalowaniem kwadratowym (N^2). Zademonstrowałem jego słabą wydajność w porównaniu z przykładowymi danymi wejściowymi w zakresie od 100 000 do 400 000 wierszy. Rozwiązanie zajęło 931 sekund, aby ukończyć dane wejściowe z 400 tys. wierszy! W tym miesiącu zacznę od krótkiego przypomnienia rozwiązania z zeszłego miesiąca i dlaczego tak źle się skaluje i działa. Następnie przedstawię podejście oparte na rewizji testu przecięcia interwałów. Takie podejście zastosowali Luca, Kamil, a być może także Daniel, co umożliwia rozwiązanie o znacznie lepszej wydajności i skalowaniu. Nazywam to rozwiązaniem zmienionymi skrzyżowaniami .

Problem z klasycznym testem skrzyżowania

Zacznijmy od szybkiego przypomnienia rozwiązania z zeszłego miesiąca.

Użyłem następujących indeksów w wejściowej tabeli dbo.Auctions, aby wspomóc obliczanie bieżących sum, które tworzą przedziały popytu i podaży:

-- Index to support solution
 
CREATE UNIQUE NONCLUSTERED INDEX idx_Code_ID_i_Quantity
  ON dbo.Auctions(Code, ID)
  INCLUDE(Quantity);
 
-- Enable batch-mode Window Aggregate
 
CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs
  ON dbo.Auctions(ID)
  WHERE ID = -1 AND ID = -2;

Poniższy kod zawiera kompletne rozwiązanie implementujące klasyczne podejście do przecięcia interwałów:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID,
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_ES_ID ON #Supply(EndSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S WITH (FORCESEEK)
    ON D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply;

Ten kod zaczyna się od obliczenia interwałów popytu i podaży i zapisania ich do tabel tymczasowych o nazwach #Demand i #Supply. Następnie kod tworzy indeks klastrowy na #Supply z EndSupply jako kluczem wiodącym, aby jak najlepiej obsługiwać test skrzyżowania. Wreszcie kod łączy #Supply i #Demand, identyfikując transakcje jako nakładające się segmenty przecinających się interwałów, przy użyciu następującego predykatu złączenia opartego na klasycznym teście przecięcia interwałów:

D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply

Plan tego rozwiązania pokazano na rysunku 1.

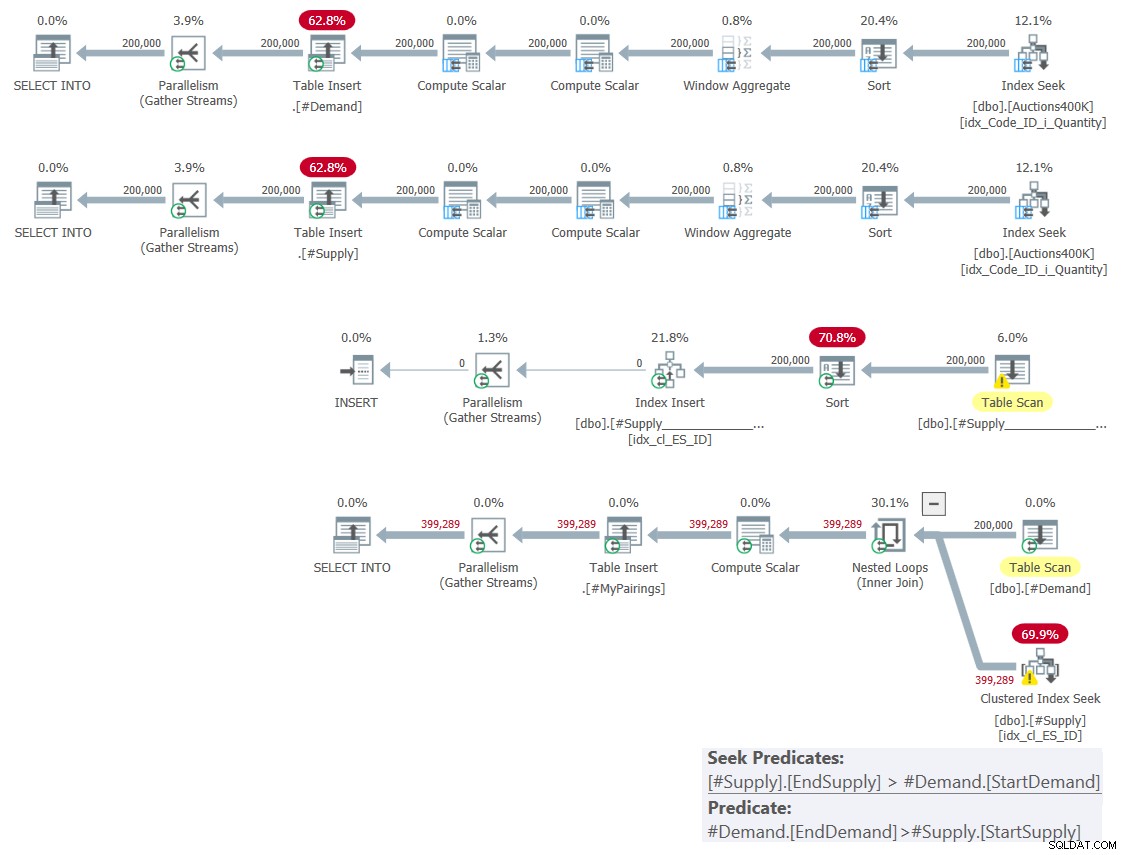Rysunek 1:Plan zapytania o rozwiązanie oparte na klasycznych skrzyżowaniach

Jak wyjaśniłem w zeszłym miesiącu, spośród dwóch predykatów zakresu, tylko jeden może być użyty jako predykat wyszukiwania w ramach operacji wyszukiwania indeksu, podczas gdy drugi musi być stosowany jako predykat rezydualny. Widać to wyraźnie w planie ostatniego zapytania na Rysunku 1. Dlatego zadałem sobie trud stworzenia tylko jednego indeksu na jednej z tabel. Wymusiłem również użycie seek w utworzonym przeze mnie indeksie za pomocą podpowiedzi FORCESEEK. W przeciwnym razie optymalizator może zignorować ten indeks i utworzyć własny przy użyciu operatora Index Spool.

Plan ten ma kwadratową złożoność, ponieważ na wiersz po jednej stronie — #Zapotrzebowanie w naszym przypadku — wyszukiwanie indeksu będzie musiało uzyskać dostęp średnio do połowy wierszy po drugiej stronie — #Podaż w naszym przypadku — na podstawie predykatu wyszukiwania i zidentyfikować ostateczne dopasowania przez zastosowanie predykatu rezydualnego.

Jeśli nadal nie jest dla ciebie jasne, dlaczego ten plan ma kwadratową złożoność, być może pomocne może być wizualne przedstawienie pracy, jak pokazano na rysunku 2.

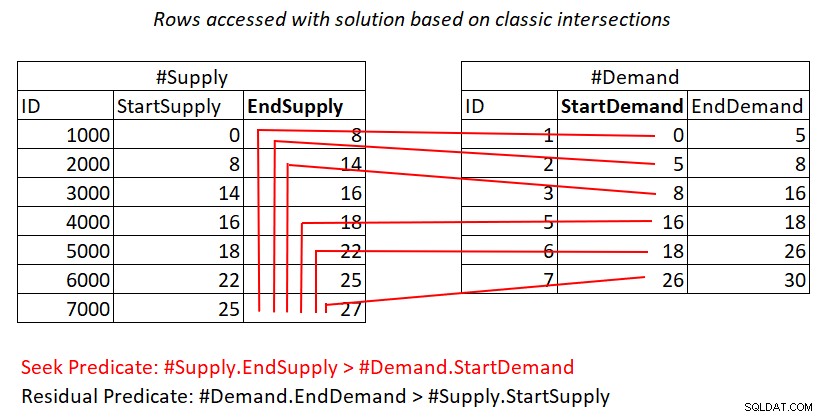Rysunek 2:Ilustracja pracy z rozwiązaniem opartym na klasycznych skrzyżowaniach

Ta ilustracja przedstawia pracę wykonaną przez sprzężenie zagnieżdżonych pętli w planie dla ostatniego zapytania. Sterta #Demand to zewnętrzne dane wejściowe sprzężenia, a indeks klastrowy na #Supply (z EndSupply jako kluczem wiodącym) to wewnętrzne dane wejściowe. Czerwone linie reprezentują czynności wyszukiwania indeksu wykonane na wiersz w #Demand w indeksie #Supply oraz wiersze, do których uzyskują dostęp w ramach skanowania zakresu w liściu indeksu. W kierunku ekstremalnie niskich wartości StartDemand w #Demand, skanowanie zakresu musi uzyskać dostęp do wszystkich wierszy w #Supply. W kierunku ekstremalnie wysokich wartości StartDemand w #Demand, skanowanie zakresu musi uzyskać dostęp do wierszy bliskich zeru w #Supply. Przeciętnie skanowanie zakresu musi uzyskać dostęp do około połowy wierszy w #Supply na wiersz w żądaniu. W przypadku wierszy popytu D i wierszy podaży S liczba dostępnych wierszy to D + D*S/2. To jest dodatek do kosztu poszukiwań, które prowadzą do pasujących wierszy. Na przykład, wypełniając dbo.Auctions 200 000 wierszy popytu i 200 000 wierszy podaży, przekłada się to na sprzężenie zagnieżdżonych pętli uzyskujące dostęp do 200 000 wierszy popytu + 200 000*200 000/2 wierszy podaży lub 200 000 + 200 000^2/2 =20 000 200 000 dostępnych wierszy. Tutaj odbywa się wiele ponownego skanowania rzędów zaopatrzenia!

Jeśli chcesz trzymać się idei przecięcia interwałów, ale uzyskać dobre wyniki, musisz wymyślić sposób na zmniejszenie ilości wykonanej pracy.

W swoim rozwiązaniu Joe Obbish podzielił interwały na wiadro w oparciu o maksymalną długość interwału. W ten sposób był w stanie zmniejszyć liczbę wierszy potrzebnych do obsługi łączeń i polegać na przetwarzaniu wsadowym. Jako filtr końcowy zastosował klasyczny test przecięcia interwałów. Rozwiązanie Joego działa dobrze, o ile maksymalna długość interwału nie jest bardzo wysoka, ale czas działania rozwiązania wydłuża się wraz ze wzrostem maksymalnej długości interwału.

Co jeszcze możesz zrobić…?

Poprawiony test skrzyżowania

Luca, Kamil i prawdopodobnie Daniel (była niejasna część dotycząca jego opublikowanego rozwiązania ze względu na formatowanie strony, więc musiałem zgadywać) zastosowali poprawiony test przecięcia interwałów, który umożliwia znacznie lepsze wykorzystanie indeksowania.

Ich test przecięcia jest alternatywą dwóch predykatów (predykaty oddzielone operatorem OR):

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >= D.StartDemand AND S.StartSupply < D.EndDemand)

W języku angielskim albo ogranicznik początku popytu przecina się z przedziałem podaży w sposób włączający, wyłączny (włączając początek i wyłączając koniec); lub ogranicznik początku podaży przecina się z przedziałem zapotrzebowania, w sposób włączający, wyłączny. Aby te dwa predykaty były rozłączne (nie miały nakładających się przypadków), ale nadal były kompletne i obejmowały wszystkie przypadki, możesz zachować operator =tylko w jednym lub drugim, na przykład:

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand)

Ten poprawiony test przecięcia interwałów jest dość wnikliwy. Każdy z predykatów może potencjalnie efektywnie korzystać z indeksu. Rozważ predykat 1:

D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
^^^^^^^^^^^^^                      ^^^^^^^^^^^^^

Zakładając, że utworzysz indeks pokrywający na #Demand z StartDemand jako kluczem wiodącym, możesz potencjalnie uzyskać połączenie zagnieżdżonych pętli, stosując pracę zilustrowaną na rysunku 3.

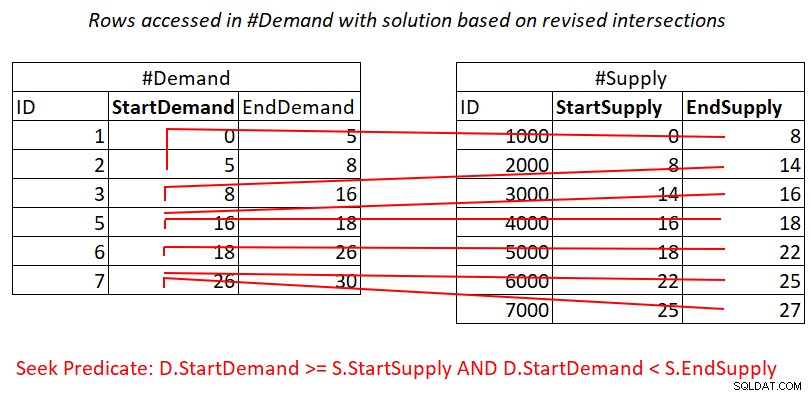
Rysunek 3:Ilustracja pracy teoretycznej wymaganej do przetworzenia predykatu 1

Tak, nadal płacisz za wyszukiwanie w indeksie #Demand na wiersz w #Supply, ale skanowanie zakresu w liściu indeksu uzyskuje dostęp do prawie rozłącznych podzbiorów wierszy. Brak ponownego skanowania wierszy!

Sytuacja jest podobna z predykatem 2:

S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand
^^^^^^^^^^^^^                     ^^^^^^^^^^^^^

Zakładając, że utworzysz indeks pokrywający #Supply z StartSupply jako kluczem wiodącym, możesz potencjalnie uzyskać połączenie zagnieżdżonych pętli, stosując pracę zilustrowaną na rysunku 4.

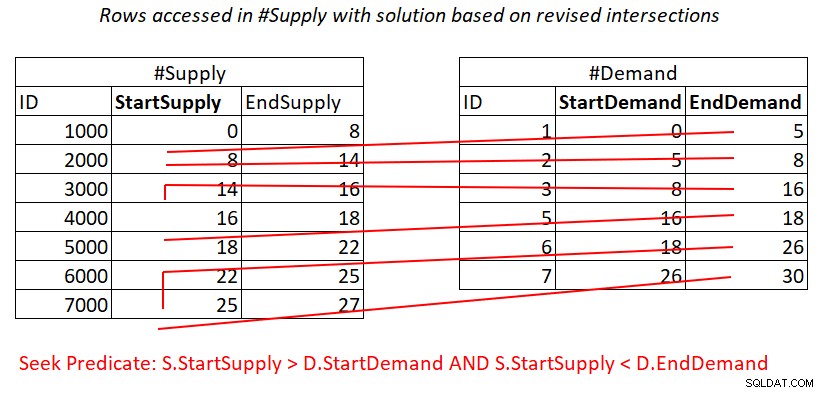
Rysunek 4:Ilustracja pracy teoretycznej wymaganej do przetworzenia predykatu 2

Również tutaj płacisz za wyszukiwanie w indeksie #Supply na wiersz w #Demand, a następnie skanowanie zakresu w liściu indeksu uzyskuje dostęp do prawie rozłącznych podzbiorów wierszy. Ponownie, bez ponownego skanowania wierszy!

Zakładając D wiersze popytu i S wiersze podaży, pracę można opisać jako:

Number of index seek operations: D  + S
Number of rows accessed:         2D + 2S

Tak więc prawdopodobnie największą część kosztów stanowi koszt I/O związany z wyszukiwaniami. Ale ta część pracy ma skalowanie liniowe w porównaniu do skalowania kwadratowego w klasycznym zapytaniu o przecięcia przedziałów.

Oczywiście należy wziąć pod uwagę wstępny koszt utworzenia indeksu na tabelach tymczasowych, który ma skalowanie log n ze względu na wymagane sortowanie, ale płacisz tę część jako wstępną część obu rozwiązań.

Spróbujmy zastosować tę teorię w praktyce. Zacznijmy od wypełnienia tymczasowych tabel #popyt i #podaży przedziałami popytu i podaży (tak samo jak w przypadku klasycznych przecięć przedziałów) i stworzenia indeksów pomocniczych:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);

Plany zapełniania tabel tymczasowych i tworzenia indeksów pokazano na rysunku 5.

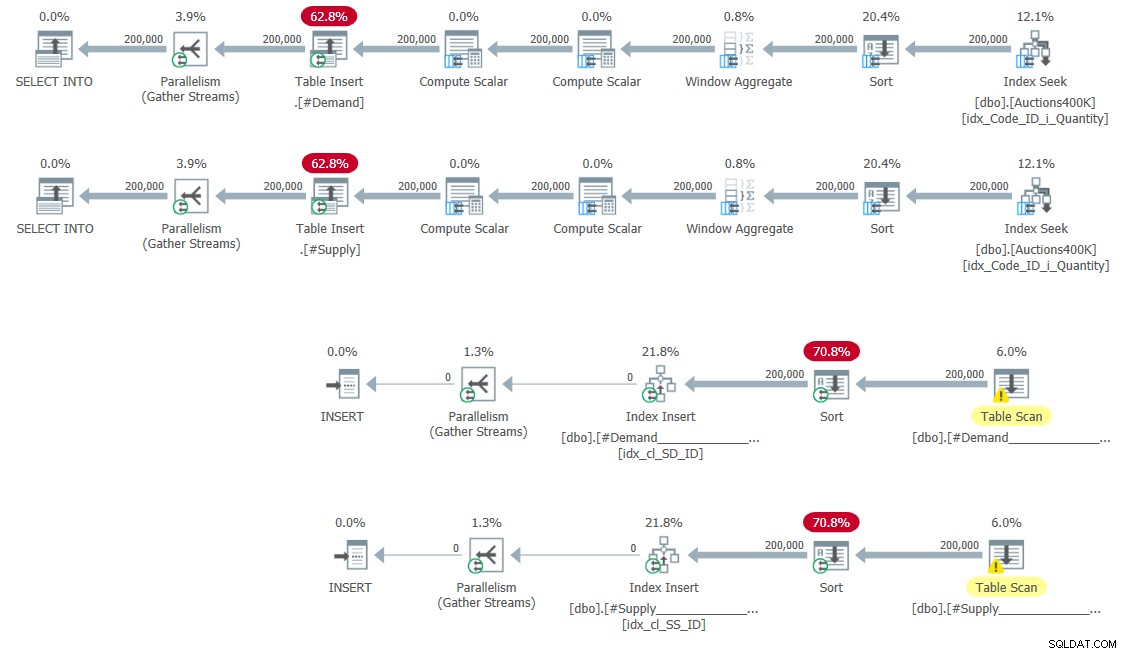
Rysunek 5:Plany zapytań dotyczące wypełniania tabel tymczasowych i tworzenia indeksy

Żadnych niespodzianek.

Przejdźmy teraz do ostatniego zapytania. Możesz pokusić się o użycie pojedynczego zapytania z wyżej wspomnianą alternatywą dwóch predykatów, na przykład:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >  D.StartDemand AND S.StartSupply < D.EndDemand);

Plan dla tego zapytania pokazano na rysunku 6.

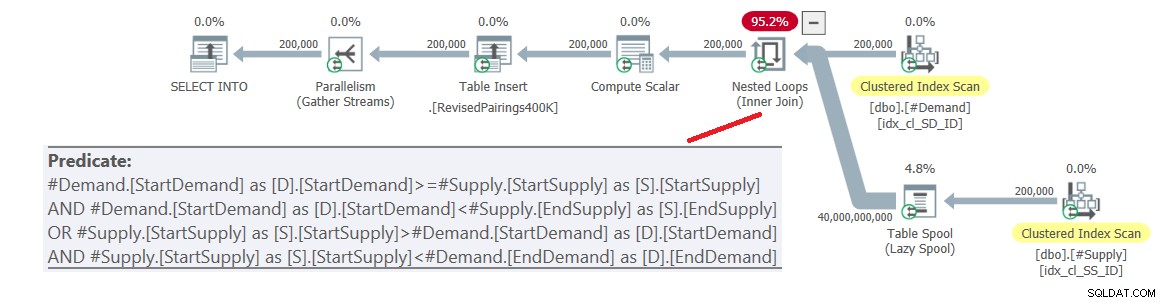
Ilustracja 6:Plan zapytania dla ostatniego zapytania przy użyciu poprawionego przecięcia test, wypróbuj 1

Problem polega na tym, że optymalizator nie wie, jak podzielić tę logikę na dwie oddzielne czynności, z których każda obsługuje inny predykat i efektywnie wykorzystuje odpowiedni indeks. Tak więc kończy się to pełnym iloczynem kartezjańskim dwóch stron, stosując wszystkie predykaty jako predykaty rezydualne. Przy 200 000 wierszy popytu i 200 000 wierszy podaży połączenie przetwarza 40 000 000 000 wierszy.

Wnikliwa sztuczka zastosowana przez Lucę, Kamila i być może Daniela polegała na rozbiciu logiki na dwa zapytania, ujednolicając ich wyniki. Właśnie wtedy ważne staje się użycie dwóch rozłącznych predykatów! Możesz użyć operatora UNION ALL zamiast UNION, unikając niepotrzebnych kosztów wyszukiwania duplikatów. Oto zapytanie implementujące to podejście:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

Plan dla tego zapytania pokazano na rysunku 7.

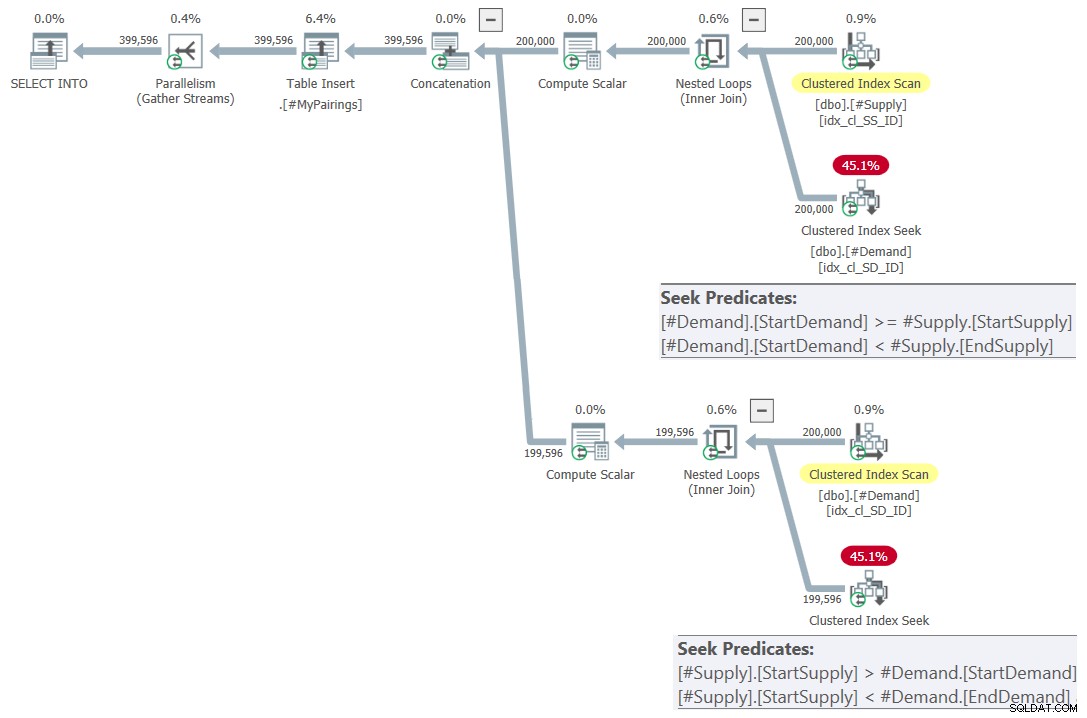
Ilustracja 7:Plan zapytania dla ostatniego zapytania przy użyciu poprawionego przecięcia test, wypróbuj 2

To jest po prostu piękne! Prawda? A ponieważ jest tak piękny, oto całe rozwiązanie od podstaw, w tym tworzenie tabel tymczasowych, indeksowanie i końcowe zapytanie:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID,
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

Jak wspomniano wcześniej, będę nazywać to rozwiązanie zmienionymi skrzyżowaniami .

Rozwiązanie Kamila

Pomiędzy rozwiązaniami Luki, Kamila i Daniela najszybszy był Kamil. Oto kompletne rozwiązanie Kamila:

SET NOCOUNT ON;
DROP TABLE IF EXISTS #supply, #demand;
GO
 
CREATE TABLE #demand
(
  DemandID           INT NOT NULL,
  DemandQuantity     DECIMAL(19, 6) NOT NULL,
  QuantityFromDemand DECIMAL(19, 6) NOT NULL,
  QuantityToDemand   DECIMAL(19, 6) NOT NULL
);
 
CREATE TABLE #supply
(
  SupplyID           INT NOT NULL,
  QuantityFromSupply DECIMAL(19, 6) NOT NULL,
  QuantityToSupply   DECIMAL(19,6) NOT NULL
);
 
WITH demand AS
(
  SELECT
    a.ID AS DemandID,
    a.Quantity AS DemandQuantity,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromDemand,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToDemand
  FROM dbo.Auctions AS a WHERE Code = 'D'
)
INSERT INTO #demand
(
  DemandID,
  DemandQuantity,
  QuantityFromDemand,
  QuantityToDemand
)
SELECT
  d.DemandID,
  d.DemandQuantity,
  d.QuantityFromDemand,
  d.QuantityToDemand
FROM demand AS d;
 
WITH supply AS
(
  SELECT
    a.ID AS SupplyID,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromSupply,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToSupply
  FROM dbo.Auctions AS a WHERE Code = 'S'
)
INSERT INTO #supply
(
  SupplyID,
  QuantityFromSupply,
  QuantityToSupply
)
SELECT
  s.SupplyID,
  s.QuantityFromSupply,
  s.QuantityToSupply
FROM supply AS s;
 
CREATE UNIQUE INDEX ix_1 ON #demand(QuantityFromDemand) 
  INCLUDE(DemandID, DemandQuantity, QuantityToDemand);
CREATE UNIQUE INDEX ix_1 ON #supply(QuantityFromSupply) 
  INCLUDE(SupplyID, QuantityToSupply);
CREATE NONCLUSTERED COLUMNSTORE INDEX nci ON #demand(DemandID) 
  WHERE DemandID is null;
 
DROP TABLE IF EXISTS #myPairings;
 
CREATE TABLE #myPairings
(
  DemandID      INT NOT NULL,
  SupplyID      INT NOT NULL,
  TradeQuantity DECIMAL(19, 6) NOT NULL
);
 
INSERT INTO #myPairings(DemandID, SupplyID, TradeQuantity) 
  SELECT
    d.DemandID,
    s.SupplyID, 
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 end
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity 
  FROM #demand AS d 
    INNER JOIN #supply AS s 
      ON (d.QuantityFromDemand < s.QuantityToSupply 
          AND s.QuantityFromSupply <= d.QuantityFromDemand)
 
  UNION ALL
 
  SELECT
    d.DemandID,
    s.SupplyID,
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 END
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
  FROM #supply AS s 
    INNER JOIN #demand AS d 
      ON (s.QuantityFromSupply < d.QuantityToDemand 
          AND d.QuantityFromDemand < s.QuantityFromSupply);

Jak widać, jest bardzo zbliżone do poprawionego rozwiązania dotyczącego skrzyżowań, które omówiłem.

Plan końcowego zapytania w rozwiązaniu Kamila przedstawia Rysunek 8.

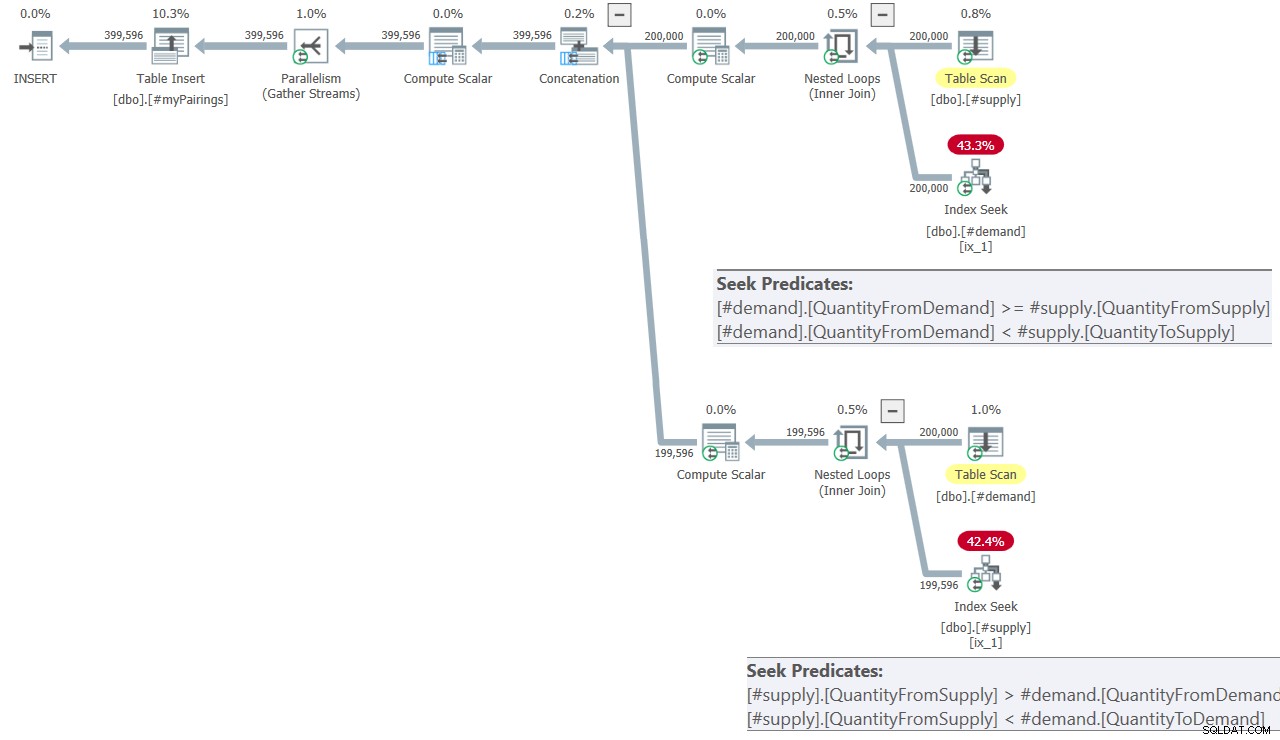
Rys. 8:Plan zapytania dla zapytania końcowego w rozwiązaniu Kamila

Plan wygląda bardzo podobnie do tego pokazanego wcześniej na rysunku 7.

Test wydajności

Przypomnijmy, że wykonanie klasycznego rozwiązania skrzyżowań zajęło 931 sekund w porównaniu z danymi wejściowymi z 400 tys. wierszy. To 15 minut! Jest znacznie, znacznie gorszy niż rozwiązanie kursora, którego ukończenie zajęło około 12 sekund na tym samym wejściu. Rysunek 9 przedstawia dane dotyczące wydajności, w tym nowe rozwiązania omówione w tym artykule.

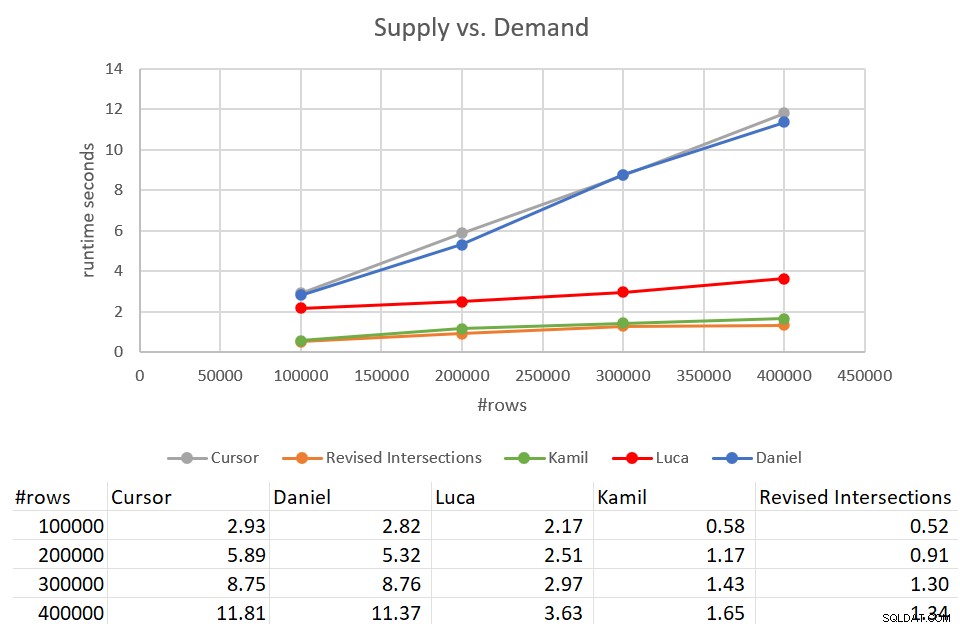
Rysunek 9:Test wydajności

Jak widać, rozwiązanie Kamila i podobne skorygowane rozwiązanie skrzyżowań zajęło około 1,5 sekundy, aby ukończyć w porównaniu z danymi wejściowymi 400 tys. To całkiem przyzwoita poprawa w porównaniu do oryginalnego rozwiązania opartego na kursorach. Główną wadą tych rozwiązań jest koszt I/O. Przy wyszukiwaniu na wiersz, dla wejścia 400 tys. wierszy, rozwiązania te wykonują ponad 1,35 mln odczytów. Ale można to również uznać za całkowicie akceptowalny koszt, biorąc pod uwagę dobry czas pracy i skalowanie, które otrzymujesz.

Co dalej?

Nasza pierwsza próba rozwiązania problemu dopasowania podaży do popytu opierała się na klasycznym teście przecięcia interwałów i uzyskała słaby plan ze skalowaniem kwadratowym. Znacznie gorzej niż rozwiązanie oparte na kursorze. Opierając się na spostrzeżeniach Luki, Kamila i Daniela, wykorzystując poprawiony test przecięcia interwałów, nasza druga próba była znaczącym ulepszeniem, które efektywnie wykorzystuje indeksowanie i działa lepiej niż rozwiązanie oparte na kursorze. Jednak to rozwiązanie wiąże się ze znacznymi kosztami we/wy. W przyszłym miesiącu będę kontynuować odkrywanie dodatkowych rozwiązań.

[ Skocz do:Oryginalne wyzwanie | Rozwiązania:Część 1 | Część 2 | Część 3 ]