W tym artykule przyjrzymy się szacowaniu selektywności i kardynalności dla predykatów w COUNT(*) wyrażenia, jak można zobaczyć w HAVING klauzule. Miejmy nadzieję, że szczegóły same w sobie są interesujące. Zapewniają również wgląd w niektóre ogólne podejścia i algorytmy stosowane przez estymator kardynalności.
Prosty przykład z wykorzystaniem przykładowej bazy danych AdventureWorks:
SELECT A.City FROM Person.[Address] AS A GROUP BY A.City HAVING COUNT_BIG(*) = 1;
Interesuje nas, w jaki sposób SQL Server uzyskuje oszacowanie dla predykatu w wyrażeniu count w HAVING klauzula.
Oczywiście HAVING klauzula to po prostu cukier składni. Równie dobrze moglibyśmy napisać zapytanie przy użyciu tabeli pochodnej lub wspólnego wyrażenia tabelowego:
-- Derived table
SELECT SQ1.City
FROM
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
) AS SQ1
WHERE SQ1.Expr1001 = 1;
-- CTE
WITH Grouped AS
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
)
SELECT G.City
FROM Grouped AS G
WHERE G.Expr1001 = 1; Wszystkie trzy formularze zapytań dają ten sam plan wykonania, z identycznymi wartościami hash planu zapytania.
Plan porealizacyjny (rzeczywisty) wykazuje doskonałe oszacowanie dla kruszywa; jednak oszacowanie dla HAVING filtr klauzul (lub odpowiednik w innych formach zapytań) jest słaby:
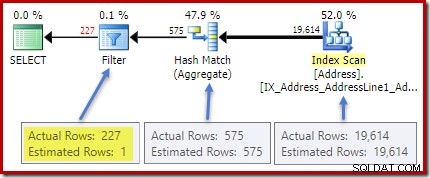
Statystyki dotyczące City kolumna zawiera dokładne informacje o liczbie różnych wartości miasta:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH DENSITY_VECTOR;
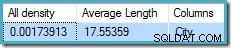
cała gęstość liczba jest odwrotnością liczby unikalnych wartości. Proste obliczenie (1 / 0,00173913) =575 podaje oszacowanie kardynalności agregatu. Grupowanie według miasta oczywiście daje jeden wiersz dla każdej odrębnej wartości.
Pamiętaj, że cała gęstość pochodzi z wektora gęstości. Uważaj, aby przypadkowo nie użyć gęstości wartość z danych wyjściowych nagłówka statystyk DBCC SHOW_STATISTICS . Gęstość nagłówka jest utrzymywana tylko w celu zapewnienia kompatybilności wstecznej; obecnie nie jest używany przez optymalizator podczas szacowania kardynalności.
Problem
Agregat wprowadza nową kolumnę obliczeniową do przepływu pracy o nazwie Expr1001 w planie wykonawczym. Zawiera wartość COUNT(*) w każdym zgrupowanym wierszu wyjściowym:
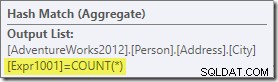
Oczywiście w bazie danych nie ma żadnych informacji statystycznych o tej nowej kolumnie obliczeniowej. Chociaż optymalizator wie, że będzie 575 wierszy, nie wie nic o dystrybucji liczby wartości w tych wierszach.
Cóż, nie całkiem nic:optymalizator zdaje sobie sprawę, że wartości liczbowe będą dodatnimi liczbami całkowitymi (1, 2, 3…). Mimo to do dokładnego oszacowania selektywności COUNT(*) = 1 potrzebny byłby rozkład tych wartości liczb całkowitych w 575 wierszach orzeczenie.
Można by pomyśleć, że z histogramu można uzyskać jakiś rodzaj informacji o rozkładzie, ale histogram dostarcza tylko konkretnych informacji o liczbie (w EQ_ROWS ) dla wartości kroku histogramu. Pomiędzy krokami histogramu mamy tylko podsumowanie:RANGE_ROWS wiersze mają DISTINCT_RANGE_ROWS odrębne wartości. W przypadku tabel, które są na tyle duże, że dbamy o jakość oszacowania selektywności, bardzo prawdopodobne jest, że większość tabeli jest reprezentowana przez podsumowania międzyetapowe.
Na przykład pierwsze dwa wiersze City histogram kolumn to:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH HISTOGRAM;

To mówi nam, że istnieje dokładnie jeden wiersz dla „Abingdon” i 29 innych wierszy po „Abingdon”, ale przed „Ballard”, z 19 różnymi wartościami w tym 29-wierszowym zakresie. Poniższe zapytanie pokazuje rzeczywisty rozkład wierszy wśród unikalnych wartości w tym 29-wierszowym zakresie międzykrokowym:
SELECT A.City, NumRows = COUNT_BIG(*) FROM Person.[Address] AS A WHERE A.City > N'Abingdon' AND A.City < N'Ballard' GROUP BY ROLLUP (A.City);

Jest 29 wierszy z 19 różnymi wartościami, tak jak powiedział histogram. Mimo to jasne jest, że nie mamy podstaw do oceny selektywności predykatu w kolumnie liczenia w tym zapytaniu. Na przykład HAVING COUNT_BIG(*) = 2 zwróci 5 wierszy (dla Aleksandrii, Altadeny, Atlanty, Augsburga i Austin), ale nie mamy możliwości określenia tego na podstawie histogramu.
Wykształcony domysł
Podejście, jakie przyjmuje SQL Server, polega na założeniu, że każda grupa jest najbardziej prawdopodobna zawierać ogólną średnią (średnią) liczbę wierszy. Jest to po prostu kardynalność podzielona przez liczbę unikalnych wartości. Na przykład dla 1000 wierszy z 20 unikalnymi wartościami SQL Server przyjmie, że (1000 / 20) =50 wierszy na grupę jest najbardziej prawdopodobną wartością.
Wracając do naszego oryginalnego przykładu, oznacza to, że kolumna obliczonej liczby „najprawdopodobniej” zawiera wartość około (19614 / 575) ~=34.1113 . Od gęstości jest odwrotnością liczby unikalnych wartości, możemy to również wyrazić jako liczność * gęstość =(19614 * 0,00173913), co daje bardzo podobny wynik.
Dystrybucja
Powiedzenie, że wartość średnia jest najprawdopodobniej prowadzi nas tylko do tej pory. Musimy również ustalić dokładnie, jak bardzo jest to prawdopodobne; i jak zmienia się prawdopodobieństwo, gdy oddalamy się od wartości średniej. Założenie, że wszystkie grupy mają dokładnie 34,113 wierszy w naszym przykładzie, nie byłoby zbyt „wykształconym” przypuszczeniem!
SQL Server obsługuje to zakładając normalną dystrybucję. Ma charakterystyczny kształt dzwonka, który być może już znasz (zdjęcie z linku w Wikipedii):
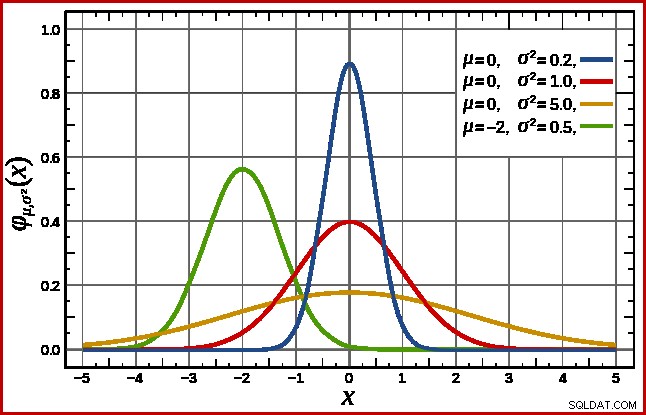
Dokładny kształt rozkładu normalnego zależy od dwóch parametrów :średnia (µ ) i odchylenie standardowe (σ ). Średnia określa położenie piku. Odchylenie standardowe określa, jak „spłaszczona” jest krzywa dzwonowa. Im bardziej płaska krzywa, tym niższy szczyt i tym bardziej gęstość prawdopodobieństwa rozkłada się na inne wartości.
SQL Server może wyprowadzić średnią z informacji statystycznych, jak już wspomniano. odchylenie standardowe obliczonych wartości kolumny licznika jest nieznana. SQL Server szacuje go jako pierwiastek kwadratowy średniej (z niewielką korektą opisaną później). W naszym przykładzie oznacza to, że dwa parametry rozkładu normalnego to w przybliżeniu 34,1113 i 5,84 (pierwiastek kwadratowy).
Standard rozkład normalny (czerwona krzywa na powyższym wykresie) jest godnym uwagi przypadkiem szczególnym. Dzieje się tak, gdy średnia wynosi zero, a odchylenie standardowe wynosi 1. Każdy rozkład normalny można przekształcić w standardowy rozkład normalny, odejmując średnią i dzieląc przez odchylenie standardowe.
Obszary i interwały
Interesuje nas szacowanie selektywności, więc szukamy prawdopodobieństwa, że wyliczona kolumna ma określoną wartość (x). To prawdopodobieństwo nie jest podane przez wartość na osi Y powyżej, ale przez obszar pod krzywą na lewo od x.
Dla rozkładu normalnego ze średnią 34,1113 i odchyleniem standardowym 5,84 pole pod krzywą na lewo od x =30 wynosi około 0,2406:
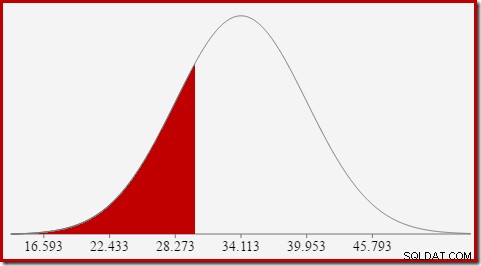
Odpowiada to prawdopodobieństwu, że kolumna obliczonej liczby jest mniejsza lub równa 30 dla naszego przykładowego zapytania.
To dobrze prowadzi do idei, że ogólnie rzecz biorąc, nie szukamy prawdopodobieństwa określonej wartości, ale przedziału . Aby znaleźć prawdopodobieństwo, że liczba równa się wartość całkowitą, musimy wziąć pod uwagę fakt, że liczby całkowite obejmują przedział o rozmiarze 1. Sposób konwersji liczby całkowitej na przedział jest nieco arbitralny. SQL Server obsługuje to, dodając i odejmując 0,5 aby podać dolną i górną granicę przedziału.
Na przykład, aby znaleźć prawdopodobieństwo, że obliczona wartość licznika wynosi 30, musimy odjąć pole pod krzywą rozkładu normalnego dla (x =29,5) od pola dla (x =30,5). Wynik odpowiada przekrojowi dla (29,5
Obszar czerwonego wycinka wynosi około 0,0533 . Zgodnie z dobrym pierwszym przybliżeniem, jest to selektywność predykatu count =30 w naszym zapytaniu testowym.
Obliczenie powierzchni w rozkładzie normalnym na lewo od danej wartości nie jest proste. Ogólny wzór wyrażony jest przez funkcję dystrybucji skumulowanej (CDF). Problem polega na tym, że CDF nie może być wyrażony za pomocą podstawowych funkcji matematycznych, więc zamiast tego należy użyć metod aproksymacji numerycznej.
Ponieważ wszystkie rozkłady normalne można łatwo przekształcić w standardowy rozkład normalny (średnia =0, odchylenie standardowe =1), wszystkie przybliżenia służą do oszacowania standardowej normy normalnej. Oznacza to, że musimy przekształcić nasze granice przedziałów od określonego rozkładu normalnego odpowiedniego dla zapytania do standardowego rozkładu normalnego. Odbywa się to, jak wspomniano wcześniej, odejmując średnią i dzieląc ją przez odchylenie standardowe.
Jeśli znasz program Excel, możesz znać funkcje ROZKŁAD.NORMALNY i ROZKŁ.NORMALNY.S, które mogą obliczać współczynniki CDF (przy użyciu metod aproksymacji numerycznej) dla określonego rozkładu normalnego lub standardowego rozkładu normalnego.
W SQL Server nie ma wbudowanego kalkulatora CDF, ale możemy go łatwo zrobić. Biorąc pod uwagę, że CDF dla standardowego rozkładu normalnego to:
…gdzie erf to funkcja błędu:
Implementacja T-SQL w celu uzyskania CDF dla standardowej dystrybucji normalnej jest pokazana poniżej. Używa aproksymacji liczbowej dla funkcji błędu to jest bardzo zbliżone do tego, którego SQL Server używa wewnętrznie:
Przykład, aby obliczyć współczynnik CDF dla x =30 przy użyciu rozkładu normalnego dla naszego zapytania testowego:
Zwróć uwagę na krok normalizacji, aby przekonwertować na standardowy rozkład normalny. Procedura zwraca wartość 0.2407196…, która dopasowuje odpowiedni wynik Excela do siedmiu miejsc po przecinku.
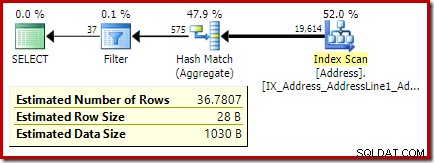
Poniższy kod modyfikuje nasze przykładowe zapytanie, aby wygenerować większe oszacowanie dla filtra (porównanie jest teraz z wartością 32, która jest znacznie bliższa średniej niż wcześniej):
Oszacowanie z optymalizatora wynosi teraz 36,7807 .
Aby ręcznie obliczyć oszacowanie, musimy najpierw zająć się kilkoma końcowymi szczegółami:
Poniższa procedura zawiera wszystkie szczegóły zawarte w tym artykule. Wymaga procedury CDF podanej wcześniej:
Możemy teraz użyć tej procedury do wygenerowania oszacowania dla naszego nowego zapytania testowego:
Dane wyjściowe to:
To bardzo dobrze wypada w porównaniu z oszacowaną kardynalnością optymalizatora wynoszącą 36,7807.
Procedurę można zastosować do innych interwałów zliczania poza testami równości. Wystarczy ustawić
Aby użyć tego w naszej procedurze, ustawiamy
Wynik to 572.5964:
Ostatni przykład użycia
Oszacowanie optymalizatora to
Od
Znowu zgadza się to z oszacowaniem optymalizatora.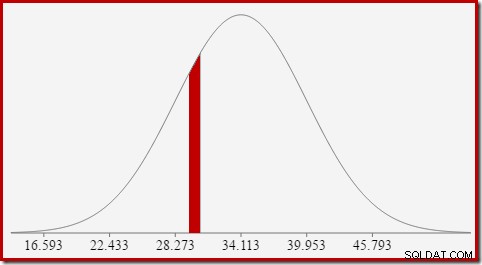
Funkcja dystrybucji skumulowanej
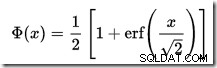
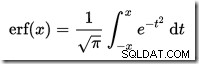
CREATE PROCEDURE dbo.GetStandardNormalCDF
(
@x float,
@cdf float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
DECLARE
@sign float,
@erf float;
SET @sign = SIGN(@x);
SET @x = ABS(@x) / SQRT(2);
SET @erf = 1;
SET @erf = @erf + (0.0705230784 * @x);
SET @erf = @erf + (0.0422820123 * POWER(@x, 2));
SET @erf = @erf + (0.0092705272 * POWER(@x, 3));
SET @erf = @erf + (0.0001520143 * POWER(@x, 4));
SET @erf = @erf + (0.0002765672 * POWER(@x, 5));
SET @erf = @erf + (0.0000430638 * POWER(@x, 6));
SET @erf = POWER(@erf, -16);
SET @erf = 1 - @erf;
SET @erf = @erf * @sign;
SET @cdf = 0.5 * (1 + @erf);
END; DECLARE @cdf float;
DECLARE @x float;
-- HAVING COUNT_BIG(*) = x
SET @x = 30;
-- Normalize 30 by subtracting the mean
-- and dividing by the standard deviation
SET @x = (@x - 34.1113) / 5.84;
EXECUTE dbo.GetStandardNormalCDF
@x = @x,
@cdf = @cdf OUTPUT;
SELECT CDF = @cdf; Końcowe szczegóły i przykłady
SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) = 32;
COUNT(*) = 1 , który nie jest tutaj szczegółowo opisany. COUNT(*) = 1 przypadku, starsze CE używa tej samej logiki, co nowe CE (dostępne w SQL Server 2014 i nowsze).CREATE PROCEDURE dbo.GetCountPredicateEstimate
(
@From integer,
@To integer,
@Cardinality float,
@Density float,
@Selectivity float OUTPUT,
@Estimate float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
BEGIN TRY
DECLARE
@Start float,
@End float,
@Distinct float,
@Mean float,
@MeanAdj float,
@Stdev float,
@NormStart float,
@NormEnd float,
@CDFStart float,
@CDFEnd float;
-- Validate input and apply defaults
IF ISNULL(@From, 0) = 0 SET @From = 1;
IF @From < 1 RAISERROR ('@From must be >= 1', 16, 1);
IF ISNULL(@Cardinality, -1) <= 0 RAISERROR('@Cardinality must be positive', 16, 1);
IF ISNULL(@Density, -1) <= 0 RAISERROR('@Density must be positive', 16, 1);
IF ISNULL(@To, 0) = 0 SET @To = CEILING(1 / @Density);
IF @To < @From RAISERROR('@To must be >= @From', 16, 1);
-- Convert integer range to interval
SET @Start = @From - 0.5;
SET @End = @To + 0.5;
-- Get number of distinct values
SET @Distinct = 1 / @Density;
-- Calculate mean
SET @Mean = @Cardinality * @Density;
-- Adjust mean;
SET @MeanAdj = @Mean * ((@Distinct - 1) / @Distinct);
-- Get standard deviation (guess)
SET @Stdev = SQRT(@MeanAdj);
-- Normalize interval
SET @NormStart = (@Start - @Mean) / @Stdev;
SET @NormEnd = (@End - @Mean) / @Stdev;
-- Calculate CDFs
EXECUTE dbo.GetStandardNormalCDF
@x = @NormStart,
@cdf = @CDFStart OUTPUT;
EXECUTE dbo.GetStandardNormalCDF
@x = @NormEnd,
@cdf = @CDFEnd OUTPUT;
-- Selectivity
SET @Selectivity =
CASE
-- Unbounded start
WHEN @From = 1 THEN @CDFEnd
-- Unbounded end
WHEN @To >= @Distinct THEN 1 - @CDFStart
-- Normal interval
ELSE @CDFEnd - @CDFStart
END;
-- Return row estimate
SET @Estimate = @Selectivity * @Distinct;
END TRY
BEGIN CATCH
DECLARE @EM nvarchar(4000) = ERROR_MESSAGE();
IF @@TRANCOUNT > 0 ROLLBACK TRANSACTION;
RAISERROR (@EM, 16, 1);
RETURN;
END CATCH;
END; DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = 32,
@To = 32,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
Przykłady przedziałów nierówności
@From i @To parametry do granic przedziałów liczb całkowitych. Aby określić nieograniczony, podaj zero lub NULL jak wolisz.SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) < 50;

@From = NULL i @To = 49 (ponieważ 50 jest wykluczone o mniej niż):DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = NULL,
@To = 49,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
BETWEEN :SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) BETWEEN 25 AND 30;

BETWEEN jest włącznie, przechodzimy procedurę @From = 25 i @To = 30 . Wynik: