Karen Ly, Jr. Fixed Income Analyst w RBC, dała mi wyzwanie T-SQL, które polega na znalezieniu najbliższego dopasowania, a nie na znalezieniu dokładnego dopasowania. W tym artykule opisuję uogólnioną, uproszczoną formę wyzwania.
Wyzwanie
Wyzwanie polega na dopasowaniu wierszy z dwóch tabel, T1 i T2. Użyj poniższego kodu, aby utworzyć przykładową bazę danych o nazwie testdb, a w niej tabele T1 i T2:
SET NOCOUNT ON;
IF DB_ID('testdb') IS NULL
CREATE DATABASE testdb;
GO
USE testdb;
DROP TABLE IF EXISTS dbo.T1, dbo.T2;
CREATE TABLE dbo.T1
(
keycol INT NOT NULL IDENTITY
CONSTRAINT PK_T1 PRIMARY KEY,
val INT NOT NULL,
othercols BINARY(100) NOT NULL
CONSTRAINT DFT_T1_col1 DEFAULT(0xAA)
);
CREATE TABLE dbo.T2
(
keycol INT NOT NULL IDENTITY
CONSTRAINT PK_T2 PRIMARY KEY,
val INT NOT NULL,
othercols BINARY(100) NOT NULL
CONSTRAINT DFT_T2_col1 DEFAULT(0xBB)
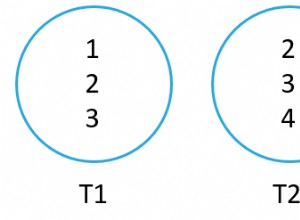
); Jak widać, zarówno T1, jak i T2 mają kolumnę numeryczną (w tym przykładzie typ INT) o nazwie val. Wyzwaniem jest dopasowanie do każdego wiersza z T1 tego wiersza z T2, gdzie bezwzględna różnica między T2.val i T1.val jest najmniejsza. W przypadku remisów (wiele pasujących wierszy w T2), dopasuj górny wiersz w oparciu o val rosnąco, keycol rosnąco. To znaczy wiersz z najniższą wartością w kolumnie val, a jeśli nadal masz powiązania, wiersz z najniższą wartością keycol. Remis służy do zagwarantowania determinizmu.
Użyj poniższego kodu, aby wypełnić T1 i T2 małymi zestawami przykładowych danych, aby móc sprawdzić poprawność swoich rozwiązań:
TRUNCATE TABLE dbo.T1;
TRUNCATE TABLE dbo.T2;
INSERT INTO dbo.T1 (val)
VALUES(1),(1),(3),(3),(5),(8),(13),(16),(18),(20),(21);
INSERT INTO dbo.T2 (val)
VALUES(2),(2),(7),(3),(3),(11),(11),(13),(17),(19); Sprawdź zawartość T1:
SELECT keycol, val, SUBSTRING(othercols, 1, 1) AS othercols FROM dbo.T1 ORDER BY val, keycol;
Ten kod generuje następujące dane wyjściowe:
keycol val othercols ----------- ----------- --------- 1 1 0xAA 2 1 0xAA 3 3 0xAA 4 3 0xAA 5 5 0xAA 6 8 0xAA 7 13 0xAA 8 16 0xAA 9 18 0xAA 10 20 0xAA 11 21 0xAA
Sprawdź zawartość T2:
SELECT keycol, val, SUBSTRING(othercols, 1, 1) AS othercols FROM dbo.T2 ORDER BY val, keycol;
Ten kod generuje następujące dane wyjściowe:
keycol val othercols ----------- ----------- --------- 1 2 0xBB 2 2 0xBB 4 3 0xBB 5 3 0xBB 3 7 0xBB 6 11 0xBB 7 11 0xBB 8 13 0xBB 9 17 0xBB 10 19 0xBB
Oto pożądany wynik dla podanych przykładowych danych:
keycol1 val1 othercols1 keycol2 val2 othercols2 ----------- ----------- ---------- ----------- ----------- ---------- 1 1 0xAA 1 2 0xBB 2 1 0xAA 1 2 0xBB 3 3 0xAA 4 3 0xBB 4 3 0xAA 4 3 0xBB 5 5 0xAA 4 3 0xBB 6 8 0xAA 3 7 0xBB 7 13 0xAA 8 13 0xBB 8 16 0xAA 9 17 0xBB 9 18 0xAA 9 17 0xBB 10 20 0xAA 10 19 0xBB 11 21 0xAA 10 19 0xBB
Zanim zaczniesz pracować nad wyzwaniem, sprawdź pożądany wynik i upewnij się, że rozumiesz logikę dopasowywania, w tym logikę rozstrzygania remisów. Rozważmy na przykład wiersz w T1, gdzie keycol to 5, a val to 5. Ten wiersz ma wiele najbliższych dopasowań w T2:
keycol val othercols ----------- ----------- --------- 4 3 0xBB 5 3 0xBB 3 7 0xBB
We wszystkich tych wierszach bezwzględna różnica między T2.val i T1.val (5) wynosi 2. Stosując logikę rozstrzygania remisów opartą na kolejności val rosnącej, keycol rosnąco najwyższy wiersz to ten, w którym val to 3, a keycol to 4.
Użyjesz małych zestawów przykładowych danych, aby sprawdzić poprawność swoich rozwiązań. Aby sprawdzić wydajność, potrzebujesz większych zestawów. Użyj poniższego kodu, aby utworzyć funkcję pomocniczą o nazwie GetNums, która generuje sekwencję liczb całkowitych w żądanym zakresie:
DROP FUNCTION IF EXISTS dbo.GetNums;
GO
CREATE OR ALTER FUNCTION dbo.GetNums(@low AS BIGINT, @high AS BIGINT) RETURNS TABLE
AS
RETURN
WITH
L0 AS (SELECT c FROM (SELECT 1 UNION ALL SELECT 1) AS D(c)),
L1 AS (SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B),
L2 AS (SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B),
L3 AS (SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B),
L4 AS (SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B),
L5 AS (SELECT 1 AS c FROM L4 AS A CROSS JOIN L4 AS B),
Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L5)
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum;
GO Użyj poniższego kodu, aby wypełnić T1 i T2 dużymi zestawami przykładowych danych:
DECLARE
@numrowsT1 AS INT = 1000000,
@maxvalT1 AS INT = 10000000,
@numrowsT2 AS INT = 1000000,
@maxvalT2 AS INT = 10000000;
TRUNCATE TABLE dbo.T1;
TRUNCATE TABLE dbo.T2;
INSERT INTO dbo.T1 WITH(TABLOCK) (val)
SELECT ABS(CHECKSUM(NEWID())) % @maxvalT1 + 1 AS val
FROM dbo.GetNums(1, @numrowsT1) AS Nums;
INSERT INTO dbo.T2 WITH(TABLOCK) (val)
SELECT ABS(CHECKSUM(NEWID())) % @maxvalT2 + 1 AS val
FROM dbo.GetNums(1, @numrowsT2) AS Nums; Zmienne @numrowsT1 i @numrowsT2 kontrolują liczbę wierszy, którymi mają być wypełnione tabele. Zmienne @maxvalT1 i @maxvalT2 kontrolują zakres różnych wartości w kolumnie val, a tym samym wpływają na gęstość kolumny. Powyższy kod wypełnia tabele po 1 000 000 wierszy i używa zakresu od 1 do 10 000 000 dla kolumny val w obu tabelach. Powoduje to niską gęstość w kolumnie (duża liczba odrębnych wartości przy niewielkiej liczbie duplikatów). Użycie niższych wartości maksymalnych spowoduje wyższą gęstość (mniejszą liczbę odrębnych wartości, a co za tym idzie więcej duplikatów).
Rozwiązanie 1, przy użyciu jednego podzapytania TOP
Najprostszym i najbardziej oczywistym rozwiązaniem jest prawdopodobnie takie, które odpytuje T1 i używając operatora CROSS APPLY stosuje zapytanie z filtrem TOP (1), porządkując wiersze według bezwzględnej różnicy między T1.val i T2.val, używając T2.val , T2.keycol jako rozstrzygający. Oto kod rozwiązania:
SELECT
T1.keycol AS keycol1, T1.val AS val1, SUBSTRING(T1.othercols, 1, 1) AS othercols1,
A.keycol AS keycol2, A.val AS val2, SUBSTRING(A.othercols, 1, 1) AS othercols2
FROM dbo.T1
CROSS APPLY
( SELECT TOP (1) T2.*
FROM dbo.T2
ORDER BY ABS(T2.val - T1.val), T2.val, T2.keycol ) AS A; Pamiętaj, że w każdej z tabel jest 1 000 000 wierszy. A gęstość kolumny val jest niska w obu tabelach. Niestety, ponieważ w zastosowanym zapytaniu nie ma predykatu filtrującego, a porządkowanie obejmuje wyrażenie manipulujące kolumnami, nie ma tutaj możliwości tworzenia indeksów pomocniczych. To zapytanie generuje plan na rysunku 1.
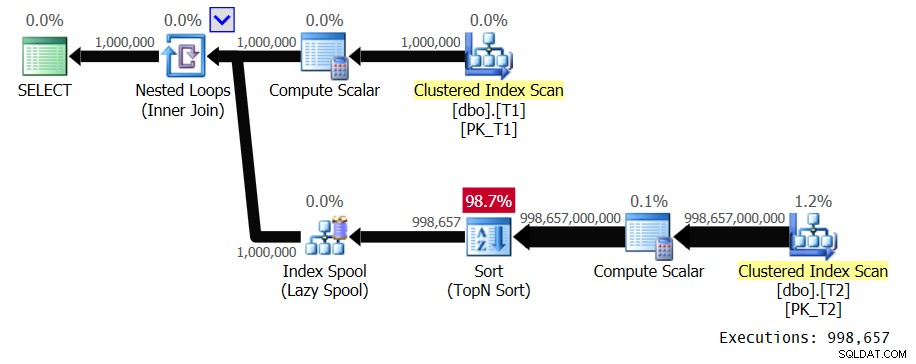Rysunek 1:Plan rozwiązania 1
Zewnętrzne wejście pętli skanuje 1 000 000 wierszy z T1. Wewnętrzne wejście pętli wykonuje pełne skanowanie T2 i sortowanie TopN dla każdej odrębnej wartości T1.val. W naszym planie dzieje się to 998 657 razy, ponieważ mamy bardzo niską gęstość. Umieszcza wiersze w buforze indeksu z kluczem T1.val, dzięki czemu może je ponownie wykorzystać do zduplikowanych wystąpień wartości T1.val, ale mamy bardzo mało duplikatów. Ten plan ma kwadratową złożoność. Pomiędzy wszystkimi oczekiwanymi wykonaniami wewnętrznej gałęzi pętli oczekuje się, że przetworzy ona blisko bilion wierszy. Mówiąc o dużej liczbie wierszy do przetworzenia zapytania, kiedy zaczniesz wymieniać miliardy wierszy, ludzie już wiedzą, że masz do czynienia z kosztownym zapytaniem. Zwykle ludzie nie wypowiadają terminów takich jak biliony, chyba że dyskutują o długu publicznym USA lub krachach giełdowych. Zazwyczaj nie zajmujesz się takimi liczbami w kontekście przetwarzania zapytań. Ale plany o kwadratowej złożoności mogą szybko skończyć się takimi liczbami. Uruchomienie zapytania w programie SSMS z włączoną opcją Uwzględnij statystyki zapytań na żywo zajęło 39,6 sekundy przetworzenie zaledwie 100 wierszy z T1 na moim laptopie. Oznacza to, że wykonanie tego zapytania powinno zająć około 4,5 dnia. Pytanie brzmi, czy naprawdę lubisz oglądać plany zapytań na żywo? To może być interesujący rekord Guinnessa do postawienia.
Rozwiązanie 2, użycie dwóch NAJLEPSZYCH podzapytań
Zakładając, że szukasz rozwiązania, którego ukończenie zajmuje kilka sekund, a nie dni, oto pomysł. W zastosowanym wyrażeniu tabelowym ujednolicić dwa wewnętrzne zapytania TOP (1) — jedno filtrujące wiersz, w którym T2.val
Oto zalecane indeksy wspierające to rozwiązanie:
CREATE INDEX idx_val_key ON dbo.T1(val, keycol) INCLUDE(othercols); CREATE INDEX idx_val_key ON dbo.T2(val, keycol) INCLUDE(othercols); CREATE INDEX idx_valD_key ON dbo.T2(val DESC, keycol) INCLUDE(othercols);
Oto kompletny kod rozwiązania:
SELECT
T1.keycol AS keycol1, T1.val AS val1, SUBSTRING(T1.othercols, 1, 1) AS othercols1,
A.keycol AS keycol2, A.val AS val2, SUBSTRING(A.othercols, 1, 1) AS othercols2
FROM dbo.T1
CROSS APPLY
( SELECT TOP (1) D.*
FROM ( SELECT TOP (1) *
FROM dbo.T2
WHERE T2.val < T1.val
ORDER BY T2.val DESC, T2.keycol
UNION ALL
SELECT TOP (1) *
FROM dbo.T2
WHERE T2.val >= T1.val
ORDER BY T2.val, T2.keycol ) AS D
ORDER BY ABS(D.val - T1.val), D.val, D.keycol ) AS A; Pamiętaj, że w każdej tabeli mamy 1 000 000 wierszy, a kolumna val ma wartości z zakresu od 1 do 10 000 000 (niska gęstość) i na miejscu znajdują się optymalne indeksy.
Plan dla tego zapytania pokazano na rysunku 2.
Rysunek 2:Plan dla rozwiązania 2
Obserwuj optymalne wykorzystanie indeksów na T2, co skutkuje planem ze skalowaniem liniowym. Ten plan używa buforu indeksu w taki sam sposób, jak poprzedni plan, tj. aby uniknąć powtarzania pracy w wewnętrznej gałęzi pętli dla zduplikowanych wartości T1.val. Oto statystyki wydajności, które uzyskałem za wykonanie tego zapytania w moim systemie:
Elapsed: 27.7 sec, CPU: 27.6 sec, logical reads: 17,304,674
Rozwiązanie 2, z wyłączonym buforowaniem
Nie możesz pomóc, ale zastanawiasz się, czy szpula indeksu jest tutaj naprawdę korzystna. Chodzi o to, aby uniknąć powtarzania pracy dla zduplikowanych wartości T1.val, ale w sytuacji takiej jak nasza, gdzie mamy bardzo niską gęstość, duplikatów jest bardzo mało. Oznacza to, że najprawdopodobniej praca związana z buforowaniem jest większa niż samo powtórzenie pracy dla duplikatów. Istnieje prosty sposób, aby to zweryfikować — za pomocą flagi śledzenia 8690 można wyłączyć buforowanie w planie, na przykład:
SELECT
T1.keycol AS keycol1, T1.val AS val1, SUBSTRING(T1.othercols, 1, 1) AS othercols1,
A.keycol AS keycol2, A.val AS val2, SUBSTRING(A.othercols, 1, 1) AS othercols2
FROM dbo.T1
CROSS APPLY
( SELECT TOP (1) D.*
FROM ( SELECT TOP (1) *
FROM dbo.T2
WHERE T2.val < T1.val
ORDER BY T2.val DESC, T2.keycol
UNION ALL
SELECT TOP (1) *
FROM dbo.T2
WHERE T2.val >= T1.val
ORDER BY T2.val, T2.keycol ) AS D
ORDER BY ABS(D.val - T1.val), D.val, D.keycol ) AS A
OPTION(QUERYTRACEON 8690); Mam plan pokazany na rysunku 3 dla tego wykonania:
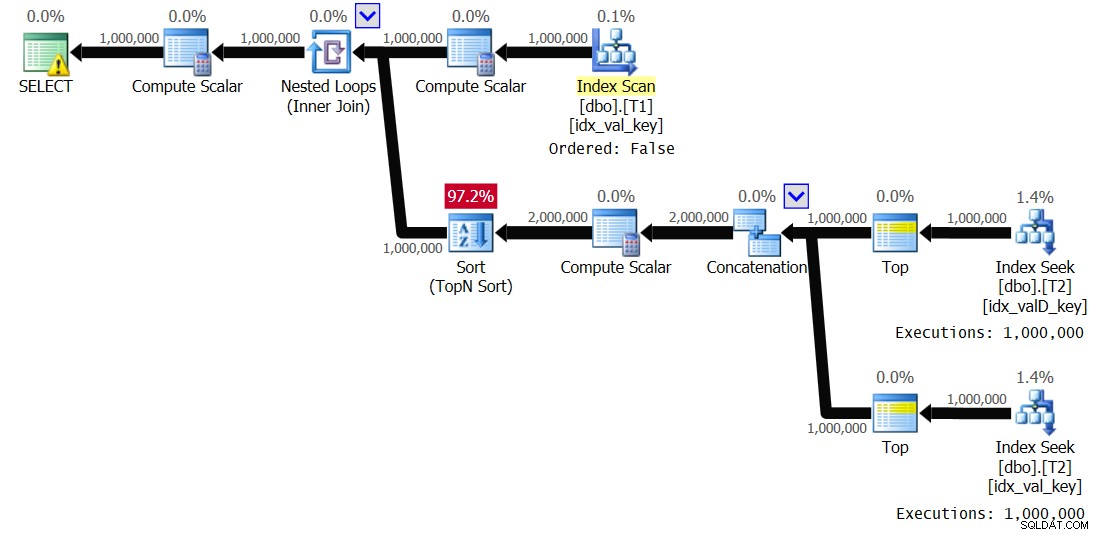Rysunek 3:Plan dla rozwiązania 2 z wyłączonym buforowaniem
Zauważ, że bufor indeksu zniknął i tym razem wewnętrzna gałąź pętli jest wykonywana 1 000 000 razy. Oto statystyki wydajności, które uzyskałem dla tego wykonania:
Elapsed: 19.18 sec, CPU: 19.17 sec, logical reads: 6,042,148
To o 44 procent skrócenie czasu wykonania.
Rozwiązanie 2, ze zmodyfikowanym zakresem wartości i indeksowaniem
Wyłączenie buforowania ma sens, gdy masz niską gęstość w wartościach T1.val; jednak zwijanie może być bardzo korzystne, gdy masz dużą gęstość. Na przykład uruchom następujący kod, aby ponownie wypełnić T1 i T2 z przykładowymi ustawieniami danych @maxvalT1 i @maxvalT2 na 1000 (1000 maksymalnych odrębnych wartości):
DECLARE
@numrowsT1 AS INT = 1000000,
@maxvalT1 AS INT = 1000,
@numrowsT2 AS INT = 1000000,
@maxvalT2 AS INT = 1000;
TRUNCATE TABLE dbo.T1;
TRUNCATE TABLE dbo.T2;
INSERT INTO dbo.T1 WITH(TABLOCK) (val)
SELECT ABS(CHECKSUM(NEWID())) % @maxvalT1 + 1 AS val
FROM dbo.GetNums(1, @numrowsT1) AS Nums;
INSERT INTO dbo.T2 WITH(TABLOCK) (val)
SELECT ABS(CHECKSUM(NEWID())) % @maxvalT2 + 1 AS val
FROM dbo.GetNums(1, @numrowsT2) AS Nums; Uruchom ponownie rozwiązanie 2, najpierw bez flagi śledzenia:
SELECT
T1.keycol AS keycol1, T1.val AS val1, SUBSTRING(T1.othercols, 1, 1) AS othercols1,
A.keycol AS keycol2, A.val AS val2, SUBSTRING(A.othercols, 1, 1) AS othercols2
FROM dbo.T1
CROSS APPLY
( SELECT TOP (1) D.*
FROM ( SELECT TOP (1) *
FROM dbo.T2
WHERE T2.val < T1.val
ORDER BY T2.val DESC, T2.keycol
UNION ALL
SELECT TOP (1) *
FROM dbo.T2
WHERE T2.val >= T1.val
ORDER BY T2.val, T2.keycol ) AS D
ORDER BY ABS(D.val - T1.val), D.val, D.keycol ) AS A; Plan tego wykonania pokazano na rysunku 4:
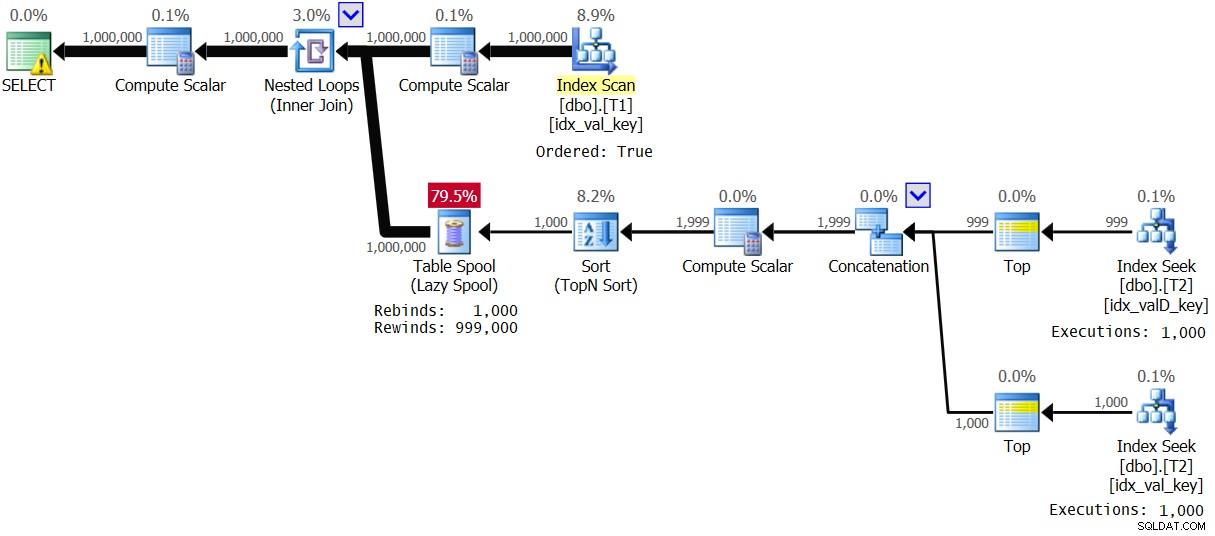Rysunek 4:Plan dla rozwiązania 2 z zakresem wartości 1–1000
Optymalizator zdecydował się na użycie innego planu ze względu na dużą gęstość w T1.val. Zauważ, że indeks na T1 jest skanowany w kolejności klucza. Tak więc, dla każdego pierwszego wystąpienia odrębnej wartości T1.val wykonywana jest wewnętrzna gałąź pętli, a wynik jest buforowany w zwykłym buforowaniu tabeli (ponowne wiązanie). Następnie dla każdego niepierwszego wystąpienia wartości stosowane jest przewijanie do tyłu. Przy 1000 różnych wartościach wewnętrzna gałąź jest wykonywana tylko 1000 razy. Skutkuje to doskonałymi statystykami wydajności:
Elapsed: 1.16 sec, CPU: 1.14 sec, logical reads: 23,278
Teraz spróbuj uruchomić rozwiązanie z wyłączonym buforowaniem:
SELECT
T1.keycol AS keycol1, T1.val AS val1, SUBSTRING(T1.othercols, 1, 1) AS othercols1,
A.keycol AS keycol2, A.val AS val2, SUBSTRING(A.othercols, 1, 1) AS othercols2
FROM dbo.T1
CROSS APPLY
( SELECT TOP (1) D.*
FROM ( SELECT TOP (1) *
FROM dbo.T2
WHERE T2.val < T1.val
ORDER BY T2.val DESC, T2.keycol
UNION ALL
SELECT TOP (1) *
FROM dbo.T2
WHERE T2.val >= T1.val
ORDER BY T2.val, T2.keycol ) AS D
ORDER BY ABS(D.val - T1.val), D.val, D.keycol ) AS A
OPTION(QUERYTRACEON 8690); Mam plan pokazany na rysunku 5.
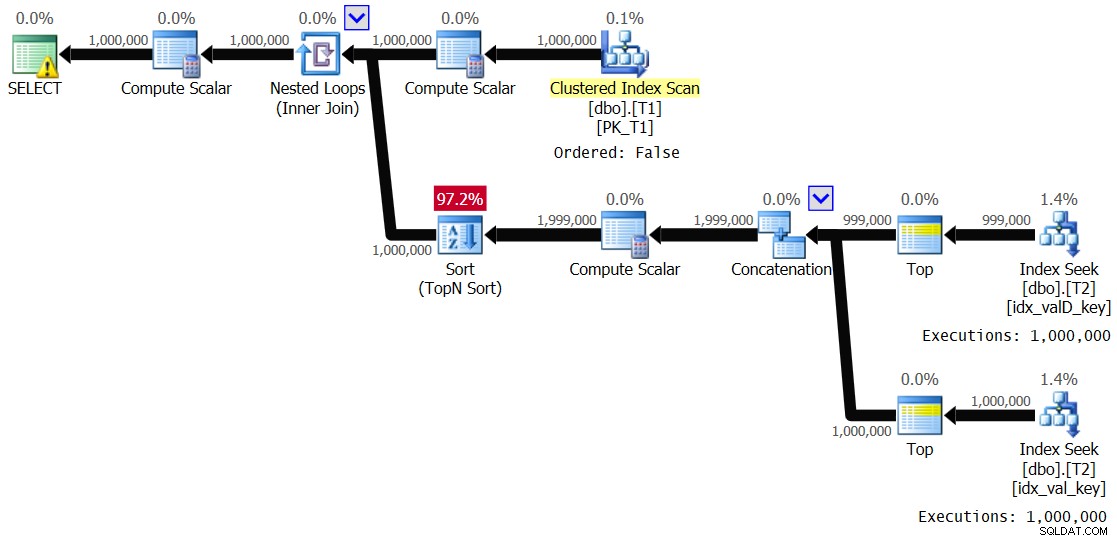Rysunek 5:Plan dla rozwiązania 2, z zakresem wartości 1 – 1000 i wyłączonym buforowaniem
Jest to zasadniczo ten sam plan, który pokazano wcześniej na rysunku 3. Wewnętrzna gałąź pętli jest wykonywana 1 000 000 razy. Oto statystyki wydajności, które uzyskałem dla tego wykonania:
Elapsed: 24.5 sec, CPU: 24.2 sec, logical reads: 8,012,548
Oczywiście chcesz uważać, aby nie wyłączać buforowania, gdy masz wysoką gęstość w T1.val.
Życie jest dobre, gdy twoja sytuacja jest na tyle prosta, że jesteś w stanie stworzyć pomocnicze indeksy. Rzeczywistość jest taka, że w niektórych przypadkach w praktyce w zapytaniu jest wystarczająco dużo dodatkowej logiki, która uniemożliwia tworzenie optymalnych indeksów pomocniczych. W takich przypadkach Rozwiązanie 2 nie zadziała dobrze.
Aby zademonstrować wydajność Rozwiązania 2 bez wspierających indeksów, ponownie wypełnij T1 i T2 z przykładowymi ustawieniami danych @maxvalT1 i @maxvalT2 na 10000000 (zakres wartości 1 – 10M), a także usuń wspierające indeksy:
DROP INDEX IF EXISTS idx_val_key ON dbo.T1;
DROP INDEX IF EXISTS idx_val_key ON dbo.T2;
DROP INDEX IF EXISTS idx_valD_key ON dbo.T2;
DECLARE
@numrowsT1 AS INT = 1000000,
@maxvalT1 AS INT = 10000000,
@numrowsT2 AS INT = 1000000,
@maxvalT2 AS INT = 10000000;
TRUNCATE TABLE dbo.T1;
TRUNCATE TABLE dbo.T2;
INSERT INTO dbo.T1 WITH(TABLOCK) (val)
SELECT ABS(CHECKSUM(NEWID())) % @maxvalT1 + 1 AS val
FROM dbo.GetNums(1, @numrowsT1) AS Nums;
INSERT INTO dbo.T2 WITH(TABLOCK) (val)
SELECT ABS(CHECKSUM(NEWID())) % @maxvalT2 + 1 AS val
FROM dbo.GetNums(1, @numrowsT2) AS Nums; Uruchom ponownie rozwiązanie 2 z włączoną opcją Dołącz statystyki zapytań na żywo w programie SSMS:
SELECT
T1.keycol AS keycol1, T1.val AS val1, SUBSTRING(T1.othercols, 1, 1) AS othercols1,
A.keycol AS keycol2, A.val AS val2, SUBSTRING(A.othercols, 1, 1) AS othercols2
FROM dbo.T1
CROSS APPLY
( SELECT TOP (1) D.*
FROM ( SELECT TOP (1) *
FROM dbo.T2
WHERE T2.val < T1.val
ORDER BY T2.val DESC, T2.keycol
UNION ALL
SELECT TOP (1) *
FROM dbo.T2
WHERE T2.val >= T1.val
ORDER BY T2.val, T2.keycol ) AS D
ORDER BY ABS(D.val - T1.val), D.val, D.keycol ) AS A; Mam plan pokazany na rysunku 6 dla tego zapytania:
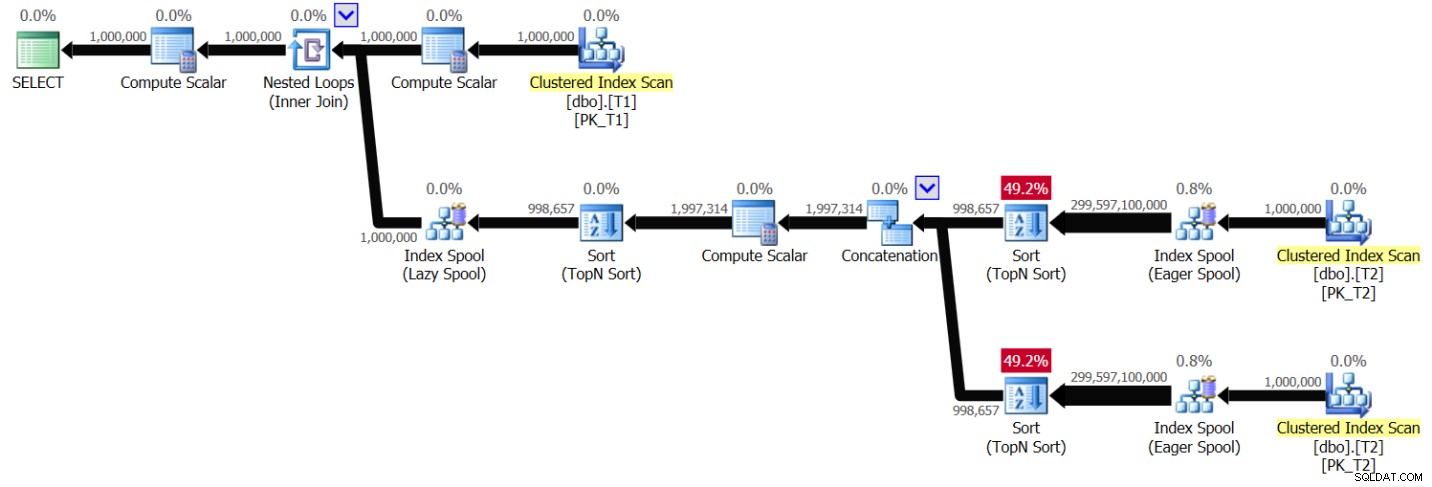Rysunek 6:Plan dla rozwiązania 2, bez indeksowania, z zakresem wartości 1 – 1 000 000
Możesz zobaczyć wzór bardzo podobny do tego pokazanego wcześniej na rysunku 1, tylko że tym razem plan skanuje T2 dwa razy dla różnej wartości T1.val. Ponownie, złożoność planu staje się kwadratowa. Uruchomienie zapytania w programie SSMS z włączoną opcją Uwzględnij statystyki zapytań na żywo zajęło 49,6 sekundy, aby przetworzyć 100 wierszy z T1 na moim laptopie, co oznacza, że wykonanie tego zapytania powinno zająć około 5,7 dnia. Może to oczywiście oznaczać dobrą wiadomość, jeśli próbujesz pobić światowy rekord Guinnessa w oglądaniu planu zapytań na żywo.
Wniosek
Chciałbym podziękować Karen Ly z RBC za przedstawienie mi tego miłego wyzwania w najbliższym meczu. Byłem pod wrażeniem jej kodu do obsługi tego, który zawierał wiele dodatkowej logiki, która była specyficzna dla jej systemu. W tym artykule przedstawiłem rozsądne rozwiązania, gdy jesteś w stanie stworzyć optymalne indeksy pomocnicze. Ale jak widać, w przypadkach, w których nie jest to możliwe, oczywiście czasy wykonania, które otrzymujesz, są fatalne. Czy możesz wymyślić rozwiązania, które sprawdzą się dobrze nawet bez optymalnych indeksów wspierających? Ciąg dalszy nastąpi…
